题目内容
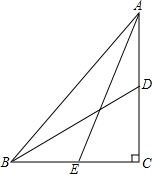已知，在Rt△ABC中，∠C=90°，E、D分别为BC、AC中点，若AE=8，BD=6，求AB的值．考点：勾股定理
专题：
分析：设BE=CE=x，AD=CD=y，再根据勾股定理列出关于x、y的方程组，求出xy的值，根据勾股定理即可得出结论．
解答：解：∵E、D分别为BC、AC中点，
∴设BE=CE=x，AD=CD=y．
∵在Rt△ABC中，∠C=90°，AE=8，BD=6，
∴
，解得
，
∴AB=
=
=
=
．
∴设BE=CE=x，AD=CD=y．
∵在Rt△ABC中，∠C=90°，AE=8，BD=6，
∴
|
|
∴AB=
| AC2+BC2 |
| 4(x2+y2) |
4(
|
4
| ||
| 3 |
点评：本题考查的是勾股定理，解答此类问题的关键是分别设出AE、CE、CD、BD的长，再根据勾股定理建立关于x、y的方程组．
练习册系列答案
相关题目
如图，移动平行四边形木架的三条边，使其构成矩形．若矩形面积是原平行四边形面积的2倍，求平行四边形两邻边的夹角α（锐角）的度数．
某片绿地的形状为四边形ABCD（如图），其中∠A=60°，AB⊥BC，AB=200m，CD=100m，求绿地周长（精确到1m）
如图，已知在?ABCD中，AB=8cm，BC=10cm，∠B=30°，求：
如图，在△ABC中，∠C=90°，D为BC边上一点，∠DAC=30°，BD=AD，且AB=2| 3 |
A、
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
如图所示，若∠3=∠1+∠2，试猜想AB与CD之间关系？
如图，根据图中所给的数据，求四边形ABCD的面积．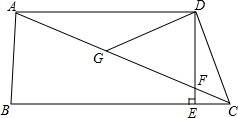
如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD=2∠ACB．