题目内容
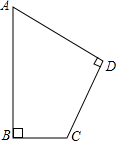 某片绿地的形状为四边形ABCD(如图),其中∠A=60°,AB⊥BC,AB=200m,CD=100m,求绿地周长(精确到1m)
某片绿地的形状为四边形ABCD(如图),其中∠A=60°,AB⊥BC,AB=200m,CD=100m,求绿地周长(精确到1m)考点:勾股定理的应用,含30度角的直角三角形
专题:
分析:延长AD,交BC的延长线于点E,则在直角△ABE与直角△CDE中,根据三角函数就可求得BE,与CE的长,就可求得AD与BC的长.
解答: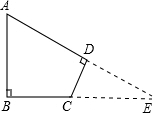 解:延长AD,交BC的延长线于点E,
解:延长AD,交BC的延长线于点E,
在Rt△ABE中,
∵AB=200m,∠A=60°,
∴BE=AB•tanA=200
m,AE=
=400m.
在Rt△CDE中,
∵CD=100m,
∴∠CED=90°-∠A=30°,
∴CE=2CD=200m,DE=
=100
m
∴AD=AE-DE=400-100
m≈227m
BC=BE-CE=200
-200≈146m
∴绿地周长=AB+AD+BC+CD=200+227+146+100=673(m).
答:绿地周长是673m.
 解:延长AD,交BC的延长线于点E,
解:延长AD,交BC的延长线于点E,在Rt△ABE中,
∵AB=200m,∠A=60°,
∴BE=AB•tanA=200
| 3 |
| AB |
| cos60° |
在Rt△CDE中,
∵CD=100m,
∴∠CED=90°-∠A=30°,
∴CE=2CD=200m,DE=
| CD |
| tan∠CED |
| 3 |
∴AD=AE-DE=400-100
| 3 |
BC=BE-CE=200
| 3 |
∴绿地周长=AB+AD+BC+CD=200+227+146+100=673(m).
答:绿地周长是673m.
点评:本题考查的是勾股定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图,试表示到点P的距离等于2.5cm的点的集合.
如图,试表示到点P的距离等于2.5cm的点的集合. 如图,已知∠AOC=108°,∠BOC=36°,试判断图中哪两个角互为补角,并说明理由.
如图,已知∠AOC=108°,∠BOC=36°,试判断图中哪两个角互为补角,并说明理由.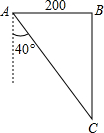 如图,东西两炮台A、B相距2000米,同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米?(精确到1米)
如图,东西两炮台A、B相距2000米,同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米?(精确到1米)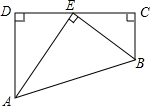 如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,则CB的长为( )
如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,则CB的长为( )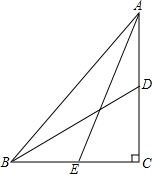 已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.
已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.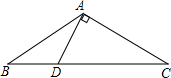 如图,在△ABC中,AB=AC,∠C=30°,DA⊥AB于点A.若BC=6cm,求BD的长.
如图,在△ABC中,AB=AC,∠C=30°,DA⊥AB于点A.若BC=6cm,求BD的长.