题目内容
 如图,根据图中所给的数据,求四边形ABCD的面积.
如图,根据图中所给的数据,求四边形ABCD的面积.考点:勾股定理
专题:
分析:首先利用勾股定理计算出CD长,然后再计算出△ADC和△ACB的面积,再求和即可.
解答:解:∵∠D=90°,
∴CD=
=
=16,
∴S△ADC=
AD•CD=
×12×16=96,
∵AC=20,CB=15,
∴S△ACB=
×AC×BC=
×20×15=150,
∴四边形ABCD的面积是:96+150=246.
∴CD=
| AC2-AD2 |
| 400-144 |
∴S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC=20,CB=15,
∴S△ACB=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形ABCD的面积是:96+150=246.
点评:此题主要考查了勾股定理,关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,试表示到点P的距离等于2.5cm的点的集合.
如图,试表示到点P的距离等于2.5cm的点的集合.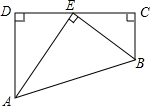 如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,则CB的长为( )
如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,则CB的长为( )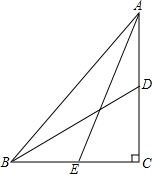 已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.
已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.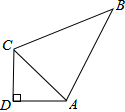 如图,四边形ABCD中,AB=13,BC=12,CD=3,AD=4,若∠D=90°,求△ABC的面积.
如图,四边形ABCD中,AB=13,BC=12,CD=3,AD=4,若∠D=90°,求△ABC的面积. 如图,四边形ABCD为⊙O的内接四边形,∠A=80°,若圆周长为18π,求
如图,四边形ABCD为⊙O的内接四边形,∠A=80°,若圆周长为18π,求
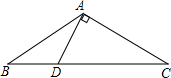 如图,在△ABC中,AB=AC,∠C=30°,DA⊥AB于点A.若BC=6cm,求BD的长.
如图,在△ABC中,AB=AC,∠C=30°,DA⊥AB于点A.若BC=6cm,求BD的长. 如图,?ABCD中,E为CD中点,连接B、E两点与AD的延长线相交于点F,若AD=5,求DF的长.
如图,?ABCD中,E为CD中点,连接B、E两点与AD的延长线相交于点F,若AD=5,求DF的长.