题目内容
 如图,在△ABC中,∠C=90°,D为BC边上一点,∠DAC=30°,BD=AD,且AB=2
如图,在△ABC中,∠C=90°,D为BC边上一点,∠DAC=30°,BD=AD,且AB=2| 3 |
A、
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
考点:勾股定理,含30度角的直角三角形
专题:
分析:首先根据直角三角形的性质可得CD=
AD,设CD=x,则AD=2x,BD=2x,根据勾股定理可得AC=
x,在Rt△ACB中利用勾股定理x的值,进而可得答案.
| 1 |
| 2 |
| 3 |
解答:解:∵∠DAC=30°,∠C=90°,
∴CD=
AD,
设CD=x,则AD=2x,BD=2x,
∴AC=
x,
在Rt△ACB中:AC2+BC2=AB2,
(
x)2+(3x)2=(2
)2,
解得:x=1,
∴AC=
,
故选:A.
∴CD=
| 1 |
| 2 |
设CD=x,则AD=2x,BD=2x,
∴AC=
| 3 |
在Rt△ACB中:AC2+BC2=AB2,
(
| 3 |
| 3 |
解得:x=1,
∴AC=
| 3 |
故选:A.
点评:此题主要考查了勾股定理,关键是正确利用x表示出CD、AD、BD、AC的长度.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,过点P分别画OA,OB的平行线交OA于点E,交OB于点F,并且用量角器量出∠PEO,∠PFO,∠AOB的大小,找找它们有哪些关系.
如图,过点P分别画OA,OB的平行线交OA于点E,交OB于点F,并且用量角器量出∠PEO,∠PFO,∠AOB的大小,找找它们有哪些关系.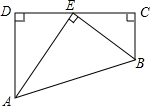 如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,则CB的长为( )
如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,则CB的长为( )
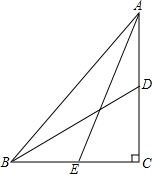 已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.
已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.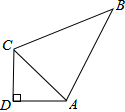 如图,四边形ABCD中,AB=13,BC=12,CD=3,AD=4,若∠D=90°,求△ABC的面积.
如图,四边形ABCD中,AB=13,BC=12,CD=3,AD=4,若∠D=90°,求△ABC的面积.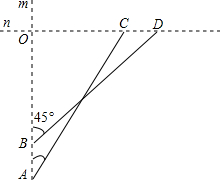 如图,在一次速度测试中,互相垂直的两条轨道m,n上各有一部测试机甲和乙,某时刻甲在A处发现乙在其北偏东30°方向的C处,3min后,甲到达B处,且发现乙在其北偏东45°方向的D处,甲又继续行驶9min到达两条轨道的交叉点O处,已知甲、乙均为匀速行驶,甲的速度是30m/min,试求乙的速度.(
如图,在一次速度测试中,互相垂直的两条轨道m,n上各有一部测试机甲和乙,某时刻甲在A处发现乙在其北偏东30°方向的C处,3min后,甲到达B处,且发现乙在其北偏东45°方向的D处,甲又继续行驶9min到达两条轨道的交叉点O处,已知甲、乙均为匀速行驶,甲的速度是30m/min,试求乙的速度.(