题目内容
 如图,移动平行四边形木架的三条边,使其构成矩形.若矩形面积是原平行四边形面积的2倍,求平行四边形两邻边的夹角α(锐角)的度数.
如图,移动平行四边形木架的三条边,使其构成矩形.若矩形面积是原平行四边形面积的2倍,求平行四边形两邻边的夹角α(锐角)的度数.考点:矩形的性质,平行四边形的性质
专题:
分析:过A作AE⊥BC于E,根据面积公式得出S平行四边形ABCD=BC×AE,S矩形ABCD=BC×AB,求出AB=2AE,根据含30度角的直角三角形的性质得出即可.
解答:解:
过A作AE⊥BC于E,
则∠AEB=90°
∵S平行四边形ABCD=BC×AE,S矩形ABCD=BC×AB,
又∵矩形面积是原平行四边形面积的2倍,
∴AB=2AE,
∴∠α=30°.

过A作AE⊥BC于E,
则∠AEB=90°
∵S平行四边形ABCD=BC×AE,S矩形ABCD=BC×AB,
又∵矩形面积是原平行四边形面积的2倍,
∴AB=2AE,
∴∠α=30°.
点评:本题考查了矩形的性质,平行四边形的性质,含30度角的直角三角形的性质的应用,能推出AB=2AE是解此题的关键,难度适中.

练习册系列答案
相关题目
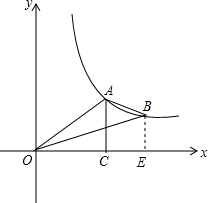 如图,点A、B在反比例函数y=
如图,点A、B在反比例函数y=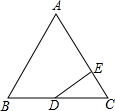 如图,△ABC是等边三角形,D为BC边的中点,DE⊥AC于点E.试探索线段CE与线段AC的数量关系,并说明理由.
如图,△ABC是等边三角形,D为BC边的中点,DE⊥AC于点E.试探索线段CE与线段AC的数量关系,并说明理由. 如图,过点P分别画OA,OB的平行线交OA于点E,交OB于点F,并且用量角器量出∠PEO,∠PFO,∠AOB的大小,找找它们有哪些关系.
如图,过点P分别画OA,OB的平行线交OA于点E,交OB于点F,并且用量角器量出∠PEO,∠PFO,∠AOB的大小,找找它们有哪些关系.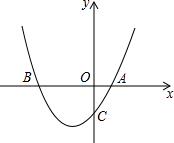 如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=-1.
如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=-1. 如图,试表示到点P的距离等于2.5cm的点的集合.
如图,试表示到点P的距离等于2.5cm的点的集合. 如图,已知∠AOC=108°,∠BOC=36°,试判断图中哪两个角互为补角,并说明理由.
如图,已知∠AOC=108°,∠BOC=36°,试判断图中哪两个角互为补角,并说明理由.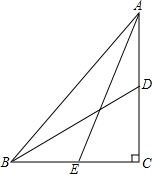 已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.
已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.