��Ŀ����
 ��ͼ���ȱߡ�ABC�ı߳�Ϊ1��PΪAB���ϵ�һ�����㣨������A��B������P��PQ��BC��Q����Q��QR��AC��R���ٹ�R��RS��AB��S����AP=x��AS=y��
��ͼ���ȱߡ�ABC�ı߳�Ϊ1��PΪAB���ϵ�һ�����㣨������A��B������P��PQ��BC��Q����Q��QR��AC��R���ٹ�R��RS��AB��S����AP=x��AS=y����1����y��x֮��ĺ�����ϵʽ����д���Ա���ȡֵ��Χ��
��2������S��P�غϵ�ΪT�����ʱx��ȡֵ��
����S��BP�ϣ���x��ȡֵ��Χ��
����S��AP�ϣ���x��ȡֵ��Χ��
��3����S��P�غϵ�ΪT����˵����S��BP��ʱ��P��S�е���һ�����ӽ�T�㣮
���㣺�ȱ������ε�����,��30�Ƚǵ�ֱ��������
ר�⣺������
��������1����AP=x����������ã�BP=1-x���ɡ�ABCΪ�ȱ������Σ�PQ��BC��Q��QR��AC��R��RS��AB��S���ó���BPQ=��CQR=��ARS=30�㣬�ó��߶�֮��Ĺ�ϵ���г�y��x�Ĺ�ϵʽ��
��2����S��P�غ�ΪTʱ����y=x���õ�x��ֵ����S��BP��ʱ����y��x���õ�0��x��
����S��AP��ʱ����y��x���õ�
��x��1��
��3����S��BP��ʱ���г�TP��ST��ʽ�ӱȽϴ�С���ɣ�
��2����S��P�غ�ΪTʱ����y=x���õ�x��ֵ����S��BP��ʱ����y��x���õ�0��x��
| 1 |
| 3 |
| 1 |
| 3 |
��3����S��BP��ʱ���г�TP��ST��ʽ�ӱȽϴ�С���ɣ�
����⣺��1����AP=x����������ã�BP=1-x��
�ߡ�ABCΪ�ȱ������Σ�PQ��BC��Q��QR��AC��R��RS��AB��S��
���BPQ=��CQR=��ARS=30�㣬
��BQ=
BP=
��QC=1-BQ=
��CR=
QC=
��AR=1-CR=
��
��AS=y��
��y=
��
=
������0��x��1��
��2����S��P�غ�ΪTʱ����y=x���õ�x=
��
��S��BP��ʱ����y��x���õ�0��x��
��
��S��AP��ʱ����y��x���õ�
��x��1��
��3����S��BP��ʱ��TP=
-x��ST=y-
=
��
-x������0��x��
ʱ����ȻST��TP������S���ӽ�T�㣮
�ߡ�ABCΪ�ȱ������Σ�PQ��BC��Q��QR��AC��R��RS��AB��S��
���BPQ=��CQR=��ARS=30�㣬
��BQ=
| 1 |
| 2 |
| 1-x |
| 2 |
| 1+x |
| 2 |
| 1 |
| 2 |
| 1+x |
| 4 |
| 3-x |
| 4 |
��AS=y��
��y=
| 1 |
| 2 |
| 3-x |
| 4 |
| 3-x |
| 8 |
��2����S��P�غ�ΪTʱ����y=x���õ�x=
| 1 |
| 3 |
��S��BP��ʱ����y��x���õ�0��x��
| 1 |
| 3 |
��S��AP��ʱ����y��x���õ�
| 1 |
| 3 |
��3����S��BP��ʱ��TP=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 8 |
| 1 |
| 3 |
| 1 |
| 3 |
������������Ҫ�����˵ȱ������ε����ʼ���30�Ƚǵ�ֱ�������Σ�����Ĺؼ��Ǹ��ݺ�30�Ƚǵ�ֱ���������ҳ��߶�֮��Ĺ�ϵ��

��ϰ��ϵ�д�
 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
�����Ŀ
 ��֪���ڡ�ABC�У�ADΪ���ߣ�FΪAB��һ�㣬CF��AD��E����֤��
��֪���ڡ�ABC�У�ADΪ���ߣ�FΪAB��һ�㣬CF��AD��E����֤��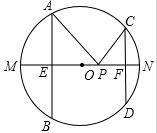 ��ͼ��AB��CD�ǰ뾶Ϊ10��ԲO�������ң�AB=16��CD=12��MN��ֱ����AB��MN�ڵ�E��CD��MN��F��PΪEF������һ�㣬��PA+PC����Сֵ��
��ͼ��AB��CD�ǰ뾶Ϊ10��ԲO�������ң�AB=16��CD=12��MN��ֱ����AB��MN�ڵ�E��CD��MN��F��PΪEF������һ�㣬��PA+PC����Сֵ��