题目内容
在△ABC中,∠A≥∠B≥∠C,且∠A=4∠B,求∠C的取值范围.
考点:三角形内角和定理
专题:
分析:把∠A和∠B都用∠C表示,再根据∠A≥∠B≥∠C即可求出∠C的范围.
解答:解:由∠A=4∠B,及∠A+∠B+∠C=180°,
得∠B=
,∠A=
,
∵∠A>∠B>∠C,
∴
≥
≥∠C,
∴∠C≤30°.
得∠B=
| 180°-∠C |
| 5 |
| 4(180°-∠C) |
| 5 |
∵∠A>∠B>∠C,
∴
| 4(180°-∠C) |
| 5 |
| 180°-∠C |
| 5 |
∴∠C≤30°.
点评:本题考查了三角形的内角和是180°,注意角的表示方法是本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,已知在?ABCD中,AE平分∠BAD,交DC于E,DF⊥BC,交AE于G,且DF=AD.
如图,已知在?ABCD中,AE平分∠BAD,交DC于E,DF⊥BC,交AE于G,且DF=AD.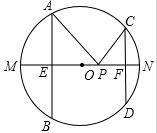 如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值.
如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值.