题目内容
设a，b，c，满足
=
，
=
，
=
，求
的值．
| ab |
| a+b |
| 1 |
| 3 |
| bc |
| b+c |
| 1 |
| 4 |
| ac |
| a+c |
| 1 |
| 5 |
| abc |
| ab+bc+ca |
考点：对称式和轮换对称式
专题：
分析：利用分式的基本性质得出
=
+
=3①，
=
+
=4②
=
+
=5③，进而求出答案．
| a+b |
| ab |
| 1 |
| a |
| 1 |
| b |
| b+c |
| bc |
| 1 |
| b |
| 1 |
| c |
| a+c |
| ac |
| 1 |
| a |
| 1 |
| c |
解答：解：∵
=
，
=
，
=
，
∴
=
+
=3①，
=
+
=4②
=
+
=5③，
①+②+③得：
2（
+
+
）=12，
故
+
+
=
=6，
则
=
．
| ab |
| a+b |
| 1 |
| 3 |
| bc |
| b+c |
| 1 |
| 4 |
| ac |
| a+c |
| 1 |
| 5 |
∴
| a+b |
| ab |
| 1 |
| a |
| 1 |
| b |
| b+c |
| bc |
| 1 |
| b |
| 1 |
| c |
| a+c |
| ac |
| 1 |
| a |
| 1 |
| c |
①+②+③得：
2（
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
故
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| ab+bc+ca |
| abc |
则
| abc |
| ab+bc+ca |
| 1 |
| 6 |
点评：此题主要考查了对称式和轮换对称式，得出2（
+
+
）=12是解题关键．
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
练习册系列答案
相关题目
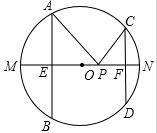如图，AB、CD是半径为10的圆O的两条弦，AB=16，CD=12，MN是直径，AB⊥MN于点E，CD⊥MN于F，P为EF上任意一点，求PA+PC的最小值．