题目内容
若x<0,则|
+
|的最小值为 .
| 1 |
| 3-|x| |
| 1 |
| |x-3| |
考点:绝对值函数的最值
专题:
分析:首先根据x的取值去掉绝对值符号,然后确定分母的最大值,从而确定代数式的最小值.
解答:解:∵x<0,
∴|x|=-x,|x-3|=3-x,
∴|
+
|=|
+
|=|
|,
∵任意实数的绝对值为非负数,
∴|
|≥0,
∴若要使原式取最小值,(x+3)(x-3)应取最大值,
∵(x+3)(3-x)=-x2+9,
∴(x+3)(3-x)有最大值为9,
∴原式有最小值
=
.
故答案为:
.
∴|x|=-x,|x-3|=3-x,
∴|
| 1 |
| 3-|x| |
| 1 |
| |x-3| |
| 1 |
| x+3 |
| 1 |
| 3-x |
| 6 |
| (x+3)(3-x) |
∵任意实数的绝对值为非负数,
∴|
| 6 |
| (x+3)(3-x) |
∴若要使原式取最小值,(x+3)(x-3)应取最大值,
∵(x+3)(3-x)=-x2+9,
∴(x+3)(3-x)有最大值为9,
∴原式有最小值
| 6 |
| 9 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查了绝对值函数的取值,解题的关键是去掉绝对值符号,难度不大.

练习册系列答案
相关题目
水池有一注水管,单开5小时,可以注满水池,另有一出水管,单开18小时可以把满池水放完,两管齐开,注满水池所用时间是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
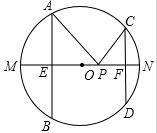 如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值.
如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值. 如图,AB∥CD,AB交MN于F,FG平分∠MFB,FH平分∠AFG,CD与MN交于E,若∠BFG:∠HFM=1:3,则∠CEM的度数是
如图,AB∥CD,AB交MN于F,FG平分∠MFB,FH平分∠AFG,CD与MN交于E,若∠BFG:∠HFM=1:3,则∠CEM的度数是 如图,长为2、宽为1的长方形ABCD以右下角的顶点C为中心顺时针旋转90°,此时A点的坐标为
如图,长为2、宽为1的长方形ABCD以右下角的顶点C为中心顺时针旋转90°,此时A点的坐标为