题目内容
2. 如图,AC平分∠BAD,CD⊥AD于点D,AB=2AD,求证:AC=BC.
如图,AC平分∠BAD,CD⊥AD于点D,AB=2AD,求证:AC=BC.
分析 过C作CE⊥AB于E,得到∠CEA=∠CDA=90°,由角平分线的定义得到∠CAD=∠CAE,根据全等三角形的性质得到AE=AD,得到AE=BE,根据线段垂直平分线的性质得到结论.
解答 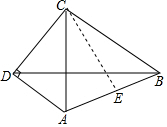 过C作CE⊥AB于E,
过C作CE⊥AB于E,
∴∠CEA=∠CDA=90°,
∵AC平分∠BAD,
∴∠CAD=∠CAE,
在△ACD与△ACE中,$\left\{\begin{array}{l}{∠CAD=∠CAE}\\{AC=AC}\\{∠D=∠AEC}\end{array}\right.$,
∴△ACD≌△ACE,
∴AE=AD,
∵AB=2AD,
∴AE=BE,
∴AC=BC.
点评 本题考查了角平分线的性质,线段垂直平分线的性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.计算(x+y)(y-x)=( )
| A. | x2-y2 | B. | x2+y2 | C. | y2-x2 | D. | (x-y)2 |
14.如表为某市居民每月用水收费标准,(单位:元/m3).
(1)某用户1月用水10立方米,共交水费23元,则a=2.3元/m3;
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费60.8元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费71元.请问该用户实际用水多少立方米?
| 用水量 | 单价 |
| 0<x≤22 | a |
| 剩余部分 | a+1.1 |
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费60.8元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费71元.请问该用户实际用水多少立方米?
11.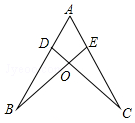 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.若分式$\frac{x+2}{x-2}$的值为0,则x的取值应满足是( )
| A. | x=-2 | B. | x≠-2 | C. | x=2 | D. | x≠2 |
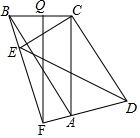 △ABC中,∠ACB=90°,BC=2,AC=4,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于F点,在旋转过程中,△ABF的面积的最大值是5.
△ABC中,∠ACB=90°,BC=2,AC=4,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于F点,在旋转过程中,△ABF的面积的最大值是5.