题目内容
10.为了倡导低碳交通,方便市民出行,某市推出了公共自行车系统,收费以小时为单位,每次使用不超过1小时的免费,超过1小时后,不足1小时的部分按1小时收费,小聪同学通过调查得知,自行车使用时间为3小时,收费2元;使用时间为4小时,收费3元.她发现当使用时间超过1小时后用车费与使用时间之间存在一次函数的关系.(1)设使用自行车的费用为y元,使用时间为x小时(x为大于1的整数),求y与x的函数解析式;
(2)若小聪此次使用公共自行车6小时,则她应付多少元费用?
(3)若小聪此次使用公共自行车付费7元,请说明她所使用的时间的范围.
分析 (1)根据题意设出y与x之间的函数关系式,然后根据题目中的数据即可求得y与x的函数解析式;
(2)将x=6代入(1)中的函数关系式即可解答本题;
(3)将y=7代入(1)中的函数关系式和根据题意可以写出她所使用的时间的范围.
解答 解:(1)设y与x的函数解析式为y=kx+b,
$\left\{\begin{array}{l}{3k+b=2}\\{4k+b=3}\end{array}\right.$,得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
即y与x的函数解析式是y=x-1;
(2)当x=6时,y=6-1=5,
即若小聪此次使用公共自行车6小时,则她应付5元费用;
(3)当y=7时,7=x-1,得x=8,
∴小聪此次使用公共自行车付费7元,说明她所使用的时间的范围是7<x≤8.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数关系式,利用一次函数的函数关系式解答问题.

练习册系列答案
相关题目
8.下列命题中,假命题的是( )
| A. | 三角形中最大的内角不能小于60° | |
| B. | 三角形的外角一定大于和它相邻的内角 | |
| C. | 等边三角形是轴对称图形,它的对称轴有3条 | |
| D. | 三角形的一条中线把该三角形分成面积相等的两个部分 |
5.下面几组数中,不相等的是( )
| A. | -3和+(-3) | B. | -5和-(+5) | C. | -7和-(-7) | D. | +2和|-2| |
19.下列计算中,正确的是( )
| A. | $\sqrt{25}=±5$ | B. | $\sqrt{(-7)^{2}=-7}$ | C. | |4-3$\sqrt{2}$|=3$\sqrt{2}$-4 | D. | ($\sqrt{2}+1$)2=3 |
20.为庆祝交通大学建校120周年,我校特别推出校庆纪念卡片,卡片有两种,一种卡片正面印着交通大学的校训,另一种卡片正面印着交通大学的校徽,两种卡片除此之外完全相同.现将3张校训卡和4张校徽正面向下放置在桌面上,随机翻出4张卡片.则下列事件是必然事件的是( )
| A. | 至少有一张是校训卡 | B. | 至少有一张是校徽卡 | ||
| C. | 翻出的卡既有校训卡又有校徽卡 | D. | 发出的卡片只有一种类型 |
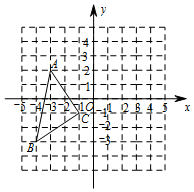 如图,(1)画出△ABC先向右平移4个单位,再向上平移1个单位后的图形△A'B'C';
如图,(1)画出△ABC先向右平移4个单位,再向上平移1个单位后的图形△A'B'C';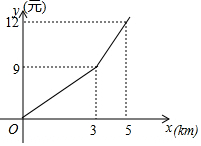 某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km.
某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km. 如图,AC平分∠BAD,CD⊥AD于点D,AB=2AD,求证:AC=BC.
如图,AC平分∠BAD,CD⊥AD于点D,AB=2AD,求证:AC=BC.