Question

14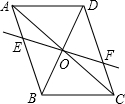．如图，在平行四边形ABCD中，对角线AC，BD交于点O，经过点O的直线交AB于E，交CD于F，
（1）求证：OE=OF；
（2）若AB=5，BC=4，OE=1.5．求四边形EFCB的周长；
（3）若S_{四边形CFEB}=10，求S_?ABCD的值．

Answer 1

分析 （1）欲证明OE=OF只要证明△AOE≌△COF即可．
（2）由四边形BCFE周长=BC+CF+EF+BE=BC+AB+EF即可计算．
（3）由△AOE≌△COF，得S_△AEO=S_△OFC，所以S_{四边形BCFE}=S_△ABC=$\frac{1}{2}$S_{平行四边形ABCD}由此即可解决问题．

解答 （1）证明：∵四边形ABCD是平行四边形，
∴AO=OC，AB∥CD，
∴∠EAO=∠FCO，
在△EAO和△FCO中，
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=OC}\\{∠AOE=∠COF}\end{array}\right.$，
∴△AOE≌△COF，
∴OE=FO．
（2）∵△AOE≌△COF，
∴OE=OF=1.5，AE=CF，
∴四边形BCFE周长=BC+CF+EF+BE=BC+AB+EF=12．
（3）∵△AOE≌△COF，
∴S_△AOE=S_△OFC，
∴S_{四边形BCFE}=S_△ABC=$\frac{1}{2}$S_{平行四边形ABCD}，
∴S_{平行四边形ABCD}=20．

点评 本题考查平行四边形的性质、全等三角形的判定和性质、四边形面积问题等知识，解题的关键是全等三角形性质的正确应用，属于中考常考题型．