题目内容
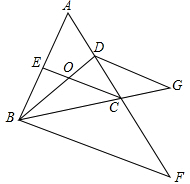 如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.
如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.考点:平行线的判定
专题:
分析:根据同角的补角相等,和平行线的判定定理即可作出判断.
解答:解:EC∥BF,DG∥BF,DG∥EC.
理由:∵∠EOD+∠OBF=180°,
又∠EOD+∠BOE=180°,
∴∠BOE=∠OBF,
∴EC∥BF;
∵∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,
∴∠DBC=∠ECB,
又∵EC∥BF,
∴∠ECB=∠CBF,
∴∠DBC=∠CBF,
又∵∠DBC=∠G,
∴∠CBF=∠G,
∴DG∥BF;
∵EC∥BF,DG∥BF,
∴DG∥EC.
理由:∵∠EOD+∠OBF=180°,
又∠EOD+∠BOE=180°,
∴∠BOE=∠OBF,
∴EC∥BF;
∵∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,
∴∠DBC=∠ECB,
又∵EC∥BF,
∴∠ECB=∠CBF,
∴∠DBC=∠CBF,
又∵∠DBC=∠G,
∴∠CBF=∠G,
∴DG∥BF;
∵EC∥BF,DG∥BF,
∴DG∥EC.
点评:本题考查了平行线的判定定理,根据同角的补角相等证明∠BOE=∠OBF是关键.

练习册系列答案
相关题目
 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
| 3x-6 |
| A、x≥-1 | B、x≠-2 |
| C、x≥2 | D、x≠2 |
 如图,Rt△ABC中,∠C=90°,AC=3,以AD为直径的半圆的面积为
如图,Rt△ABC中,∠C=90°,AC=3,以AD为直径的半圆的面积为| 25π |
| 8 |
| A、2 | B、4 | C、5 | D、2π |
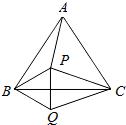 如图所示,点P是等边三角形ABC内的一点,连接PA、PB、PC以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
如图所示,点P是等边三角形ABC内的一点,连接PA、PB、PC以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.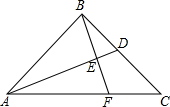 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D为BC边的中点,BE⊥AD于点E,交AC于点F,求
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D为BC边的中点,BE⊥AD于点E,交AC于点F,求 E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长.
E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长. 如图,一菱形ABCD的边长为2,且∠ABC=120°,点E是BC的中点,点P为BD上一点,且△PCE的周长最小.
如图,一菱形ABCD的边长为2,且∠ABC=120°,点E是BC的中点,点P为BD上一点,且△PCE的周长最小.  当∠1,∠2,∠3满足条件
当∠1,∠2,∠3满足条件