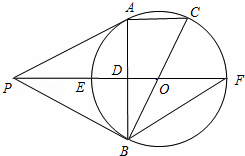
题目内容
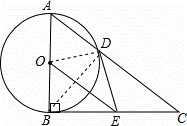
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)试探究线段CD、DE、EO之间的等量关系,并加以证明;
(2)若tanC=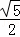 ,DE=2,求AD的长.
,DE=2,求AD的长.
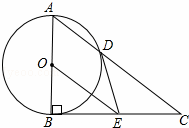
解:(1)DE与⊙O相切.理由如下:连接OD,BD.
∵AB是直径,
∴∠ADB=∠BDC=90°.
∵E是BC的中点,
∴DE=BE=CE.
∴∠EBD=∠EDB.
∵OD=OB,∴∠OBD=∠ODB.∴∠EDO=∠EBO=90°.
∴DE与⊙O相切.
(2)由题意,可得OE是△ABC的中位线,
∴AC=2OE.
∵∠ABC=∠BDC=90°,∠C=∠C,
∴△ABC∽△BDC.
∴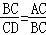 ,即BC2=CD•AC.
,即BC2=CD•AC.
∵BC=2EB=2DE,AC=2EO,
∴4DE2=CD•2EO.
即2DE2=CD•EO.
(3)∵tanC=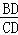 =
=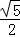 ,可设BD=
,可设BD=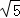 x,CD=2x,
x,CD=2x,
∵在Rt△BCD中,BC=2DE=4,BD2+CD2=BC2.
∴(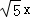 )2+(2x)2=16.
)2+(2x)2=16.
解得:x=±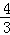 (负值舍去).
(负值舍去).
∴BD=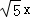 =
=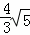 .
.
∵∠ABD=∠C,
∴tan∠ABD=tanC.
∴AD=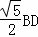 =
=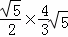 =
=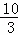 .
.
答:AD的长是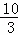 .
.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

 B.
B.  C.
C.  D.
D. 


 B.
B.  C.
C.  D.
D. 
 .
.
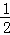 ,求⊙O的直径.
,求⊙O的直径.