题目内容
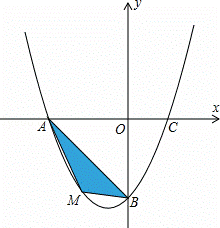
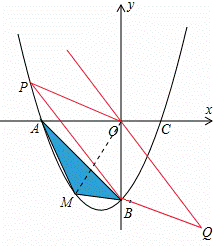
在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
解:(1)设此抛物线的函数解析式为:
y=ax2+bx+c(a≠0),
将A(﹣4,0),B(0,﹣4),C(2,0)三点代入函数解析式得:
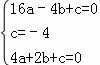
解得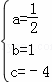 ,
,
所以此函数解析式为:y=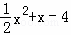 ;
;
(2)∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m,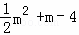 ),
),
∴S=S△AOM+S△OBM﹣S△AOB
=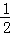 ×4×(﹣
×4×(﹣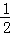 m2﹣m+4)+
m2﹣m+4)+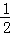 ×4×(﹣m)﹣
×4×(﹣m)﹣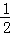 ×4×4
×4×4
=﹣m2﹣2m+8﹣2m﹣8
=﹣m2﹣4m,
=﹣(m+2)2+4,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4.
答:m=﹣2时S有最大值S=4.
(3)设P(x,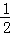 x2+x﹣4).
x2+x﹣4).
当OB为边时,根据平行四边形的性质知PB∥OQ,
∴Q的横坐标的绝对值等于P的横坐标的绝对值,
又∵直线的解析式为y=﹣x,
则Q(x,﹣x).
由PQ=OB,得|﹣x﹣(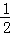 x2+x﹣4)|=4,
x2+x﹣4)|=4,
解得x=0,﹣4,﹣2±2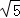 .
.
x=0不合题意,舍去.
如图,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=﹣x得出Q为(4,﹣4).
由此可得Q(﹣4,4)或(﹣2+2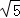 ,2﹣2
,2﹣2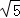 )或(﹣2﹣2
)或(﹣2﹣2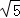 ,2+2
,2+2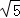 )或(4,﹣4).
)或(4,﹣4).

练习册系列答案
相关题目

 ,
, ,
, ,…,观察上面的计算过程,寻找规律并计算C106= .
,…,观察上面的计算过程,寻找规律并计算C106= . ,DE=2,求AD的长.
,DE=2,求AD的长.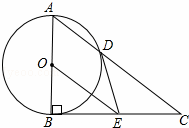
 的解集在数轴上表示为( )
的解集在数轴上表示为( ) B.
B.  C.
C.  D.
D. 
 +
+ =
=