题目内容
19.下列图形中:①平行四边形;②矩形;③等边三角形;④圆.
其中既是中心对称图形又是轴对称图形的共有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据中心对称图形与轴对称图形的概念进行判断即可.
解答 解:矩形、圆既是中心对称图形又是轴对称图形,
平行四边形是中心对称图形,不是轴对称图形,
等边三角形不是中心对称图形,是轴对称图形,
故选:B.
点评 本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.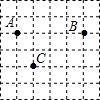 吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )
吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )
 吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )
吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (-1,-1) |
11.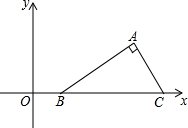 如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
 如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )| A. | (-4,-2-$\sqrt{3}$) | B. | (-4,-2+$\sqrt{3}$) | C. | (-2,-2+$\sqrt{3}$) | D. | (-2,-2-$\sqrt{3}$) |
8.一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
| 销售方式 | 粗加工后销售 | 精加工后销售 |
| 每吨获利(元) | 1000 | 2000 |
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
1.x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,则(1+$\frac{1}{y}$)(1-$\frac{1}{x}$)=( )
| A. | $4\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{3}{2}$ |
 如图,已知在Rt△ABC中,AB=AC=$\frac{3\sqrt{2}}{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2016个内接正方形的边长为($\frac{1}{2}$)2015.
如图,已知在Rt△ABC中,AB=AC=$\frac{3\sqrt{2}}{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2016个内接正方形的边长为($\frac{1}{2}$)2015.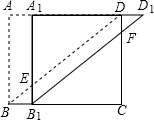 如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1,点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.
如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1,点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.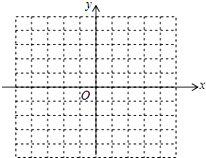 在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出将△ABC向右平移3个单位得到的△A1B1C1.
在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出将△ABC向右平移3个单位得到的△A1B1C1.