题目内容
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A. 频率就是概率
B. 频率与试验次数无关
C. 概率是随机的,与频率无关
D. 随着试验次数的增加,频率一般会越来越接近概率
D
【解析】因为大量重复试验事件发生的频率逐渐稳定到某个常数附近，可以用这个常数估计这个事件发生的概率,所以D选项说法正确,故选D.
倡导健康生活，推进全民健身，某社区要购进A、B两种型号的健身器材若干套，A、B两种型号健身器材的购买单价分别为每套310元，460元，且每种型号健身器材必须整套购买．
(1)若购买A、B两种型号的健身器材共50套，且恰好支出20000元，求A、B两种型号健身器材各购买多少套？
(2)若购买A、B两种型号的健身器材共50套，且支出不超过18000元，求A种型号健身器材至少要购买多少套？
（1）购买A种型号健身器材20套，B型器材健身器材30套； （2）A种型号健身器材至少要购买34套．
【解析】试题分析：（1）设购买A种型号健身器材x套，B型器材健身器材y套，根据题目中的“A，B两种型号的健身器材共50套、共支出20000元”可列方程组，解方程组即可；（2）设购买A型号健身器材m套，根据“A型器材总费用+B型器材总费用≤18000”，列不等式求解即可．
试题解析：（1... 下列命题中，其逆命题为真命题的是（ ）
A. 若a＝b，则a2＝b2 B. 同位角相等
C. 两边和一角对应相等的两个三角形全等 D. 等腰三角形两底角不相等
C
【解析】根据互为逆命题的关系，题设和结论互换，可知：
若a=b，则a2＝b2的逆命题为：若a2＝b2，则a=b，是假命题；
同位角相等的逆命题为：相等的角是同位角，是假命题；
两边和一角对应相等的两个三角形全等的逆命题是：全等三角形的对应边相等，对应角相等，是真命题；
等腰三角形的两底角不相等的逆命题为：两个角不相等的三角形是等腰三角形，是假命题.
故选：C... 计算：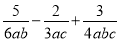 
= ．
【解析】试题分析：原式＝
＝．
故答案为： ． 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
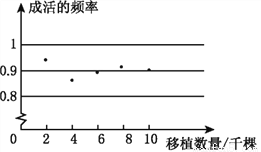
(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
（1）0.9附近，0.9；（2）①4.5，15万棵.
【解析】（1）由图可知，成活概率在0.9上下波动，故可估计这种树苗成活的频率稳定在0.9，成活的概率估计值为0.9；
（2）①5×成活率即为所求的成活的树苗棵树；
②方法1:利用成活率求得需要树苗棵树，减去已移植树苗数即为所求的树苗的棵树；
方法2：设还需移植这种树苗万棵，根据成活率及成活总数列出方程即可。 小明练习射击,共射击600次,其中有380次击中靶子,由此可估计,小明射击一次击中靶子的概率是( )
A. 38% B. 60%
C. 63% D. 无法确定
C
【解析】根据频率=频数÷数据总数计算,因为小明练习射击,共射击600次,其中有380次击中靶子,所以射中靶子的频率=380÷600≈0.63,故小明射击一次击中靶子的概率是约63%,故选C. 下列命题中，其逆命题成立的是__．（只填写序号）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形．
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题，再分析逆命题是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案。
①两直线平行，同旁内角互补，正确；
②如果两个角相等，那么它们是直角，错误；
③如果两个实数的平方相等，那么这两个实数相等，错误；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形，正确．
... 在平行四边形ABCD中，∠B＝60°，那么下列各式中，不能成立的是( )
A．∠D＝60°
B．∠A＝120°
C．∠C＋∠D＝180°
D．∠C＋∠A＝180°
D
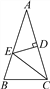
【解析】∵四边形ABCD是平行四边形，∴∠D＝∠B＝60°．故A正确；∵AD∥BC，∴∠C＋∠D＝180°，故C正确；∵AD∥BC，∴∠A＋∠B＝180°，∴∠A＝180°－∠B＝120°，故B正确；∵四边形ABCD是平行四边形，∴∠C＝∠A＝120°，故D不正确，故选D． 如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC.
求∠ECD的度数；
36°
【解析】试题分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AE=CE，然后根据等边对等角可得∠ECD=∠A；
试题解析：
∵ED垂直平分AC，
∴AE=CE，
∴∠ECD=∠A，
∵∠A=36°，
∴∠ECD=36°；