题目内容
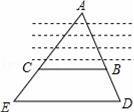
如图1,抛物线y=a(x﹣1)2+4与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,直线MD⊥x轴于点D,E是线段DM上一点,DE=1,且∠DBE=∠BMD.
(1)求抛物线的解析式;
(2)P是抛物线上一点,且△PBE是以BE为一条直角边的直角三角形,请求出所有符合条件的P点的坐标;
(3)如图2,N为线段MD上一个动点,以N为等腰三角形顶角顶点,NA为腰构造等腰△NAG,且G点落在直线CM上,若在直线CM上满足条件的G点有且只有一个时,求点N的坐标.


【考点】二次函数综合题;待定系数法求一次函数解析式;勾股定理;相似三角形的判定与性质.
【专题】综合题.
【分析】(1)由∠DBE=∠BMD可得△BDE∽△MDB,然后根据相似三角形的性质可求出DB,从而得到点B的坐标,然后把点B的坐标代入抛物线的解析式,就可解决问题;
(2)可分点E和点B为直角顶点两种情况进行讨论:①点E为直角顶点,作EF⊥EB交x轴于点F,交抛物线于点P1、P2,如图1,易证△FDE∽△EDB,根据相似三角形的性质可求出DF的值,从而可求出点F的坐标,然后用待定系数法求出直线EF的解析式,再求出直线EF与抛物线的交点,就可解决问题;②点B为直角顶点,先求出BP3的解析式,再求出直线BP3与抛物线的交点,就可解决问题;
(3)作NG⊥MC于G,作CH⊥MD于H,如图2.设N(1,n),易得NG=
 MN=
MN=
 (4﹣n),NA2=22+n2=4+n2,由题可得NG=NA,由此即可得到关于n的方程,解这个方程就可解决问题.
(4﹣n),NA2=22+n2=4+n2,由题可得NG=NA,由此即可得到关于n的方程,解这个方程就可解决问题.
【解答】解:(1)由题可知:M(1,4),
则有OD=1,DM=4.
∵∠DBE=∠BMD,∠BDE=∠MDB,
∴△BDE∽△MDB,
∴
 =
=
 ,
,
∵DE=1,DM=4,
∴
 =
=
 ,
,
解得:DB=2,
∴OB=OD+DB=3,
∴B(3,0).
把点B(3,0)代入y=a(x﹣1)2+4,得
a(3﹣1)2+4=0,
解得:a=﹣1.
∴抛物线的解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3;
(2)①当∠PEB=90°时,
作EF⊥EB交x轴于点F,交抛物线于点P1、P2,如图1,
则有∠FEB=∠FED+∠DEB=90°.
∵∠FED+∠EFD=90°,
∴∠EFD=∠DEB.
∵∠FDE=∠EDB=90°,
∴△FDE∽△EDB,
∴
 =
=
 ,
,
∴
 =
=
 ,
,
解得:DF=
 ,
,
∴OF=OD﹣DF=1﹣
 =
=
 ,
,
∴F(
 ,0).
,0).
设直线EF的解析式为y=kx+b,
则有
 ,
,
解得:
 ,
,
∴直线EF的解析式为:y=2x﹣1.
联立
 ,
,
解得:
 或
或
 ,
,
∴P1(2,3),P2(﹣2,﹣5);
②当∠PBE=90°时,
可设直线BP3的解析式为:y=2x+n,
把B(3,0)代入y=2x+n,得
6+n=0,
解得:n=﹣6,
∴直线BP3的解析式为y=2x﹣6,
联立
 ,
,
解得:
 或
或
 ,
,
∴P3(﹣3,﹣12).
综上所述:符合条件的P点的坐标为P1(2,3),P2(﹣2,﹣5),P3(﹣3,﹣12);
(3)作NG⊥MC于G,作CH⊥MD于H,如图2.
则有∠MGN=∠MHC=90°.
设N(1,n),
当x=0时,y=3,点C(0,3).
∵M(1,4),
∴CH=MH=1,
∴∠CMH=∠MCH=45°,
∴NG=
 MN=
MN=
 (4﹣n).
(4﹣n).
在Rt△NAD中,
∵AD=DB=2,DN=n,
∴NA2=22+n2=4+n2.
当直线CM上满足条件的G点有且只有一个时,有NG=NA,
∴
 (4﹣n)2=4+n2
(4﹣n)2=4+n2
整理得:n2+8n﹣8=0,
解得:n1=﹣4+2
 ,n2=﹣4﹣2
,n2=﹣4﹣2
 (舍负),
(舍负),
∴N(1,﹣4+2
 ).
).




【点评】本题主要考查了运用待定系数法求直线及抛物线的解析式、相似三角形的判定与性质、解一元二次方程、勾股定理、求直线与抛物线的交点坐标等知识,用到了分类讨论的思想,利用NG=NA则是解决第(3)小题的关键.

 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
| 解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.



 图象的每条曲线上,y都随x的增大而增大,则k的取值范围是( )
图象的每条曲线上,y都随x的增大而增大,则k的取值范围是( )