题目内容
学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
| 解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.
【考点】解一元二次方程-因式分解法;解一元二次方程-配方法.
【专题】阅读型.
【分析】(1)移项,提取公因式分解成两个一元一次方程,解一元一次方程即可求得;
(2)整理后,把常数项移项后,在左右两边同时加上一次项系数的一半的平方.
【解答】解:(1)正确,
(2)错误,
改正:整理,得x2﹣2x﹣10=0,
配方,得(x﹣1)2=11,
∴x﹣1= ,
,
∴x1=1 ,x2=1﹣
,x2=1﹣ .
.
【点评】本题考查了解一元二次方程的应用,熟练掌握解一元二次方程的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
| x | … | 0 | 1 | 2 | … |
| y | … | 4 | ﹣4 | 6 | … |
(1)ac<0;(2)当x>1时,y的值随x值得增大而增大;(3)﹣1是方程ax2+bx+c=0的一个根;(4)当﹣1<x<2时,ax2+bx+c<0,其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
 B.
B. C.
C.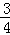 D.
D.

 ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.

 B.
B.
 C.
C.
 D.
D.


 是AC的中点.若AD=6,DE=5,则CD的长等于 .
是AC的中点.若AD=6,DE=5,则CD的长等于 .