题目内容
13. 如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“美好点”.如图2,⊙O的半径为2,点B在⊙O上,∠BOA=60°,OA=4,若点A′、B′分别是点A,B关于⊙O的美好点,求A′B′的长.
如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“美好点”.如图2,⊙O的半径为2,点B在⊙O上,∠BOA=60°,OA=4,若点A′、B′分别是点A,B关于⊙O的美好点,求A′B′的长.
分析 设OA交⊙O于C,连结B′C,如图2,根据新定义计算出OA′,OB′,则点A′为OC的中点,点B和B′重合,再证明△OBC为等边三角形,则B′A′⊥OC,然后在Rt△OA′B′中,利用正弦的定义可求A′B′的长.
解答  解:设OA交⊙O于C,连结B′C,如图2,
解:设OA交⊙O于C,连结B′C,如图2,
∵OA′•OA=22,
而r=2,OA=4,
∴OA′=1,
∵OB′•OB=22,
∴OB′=2,即点B和B′重合,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴B′A′⊥OC,
在Rt△OA′B′中,sin∠A′OB′=$\frac{A'B'}{OB'}$,
∴A′B′=2sin60°=$\sqrt{3}$.
点评 本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.也考查了阅读理解能力.

练习册系列答案
相关题目
4.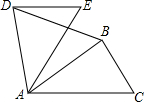 如图,如果△ABC绕点A逆时针方向旋转60°后得到△ADE,且AB=2,那么BD的长为( )
如图,如果△ABC绕点A逆时针方向旋转60°后得到△ADE,且AB=2,那么BD的长为( )
 如图,如果△ABC绕点A逆时针方向旋转60°后得到△ADE,且AB=2,那么BD的长为( )
如图,如果△ABC绕点A逆时针方向旋转60°后得到△ADE,且AB=2,那么BD的长为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
8.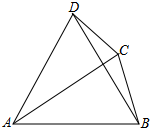 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )| A. | 18° | B. | 20° | C. | 25° | D. | 15° |
3.下列点不在正比例函数$y=-\frac{1}{2}x$的图象上的是( )
| A. | (0,0) | B. | (2,-1) | C. | (-1,2) | D. | (-2,1) |
 如图,△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,若四边形DEFG是有一边长落在AB边上的正方形,另两顶点分别在AC、BC边上,请在网格中作出图形,并计算四边形DEFG的面积是$\frac{144}{49}$.
如图,△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,若四边形DEFG是有一边长落在AB边上的正方形,另两顶点分别在AC、BC边上,请在网格中作出图形,并计算四边形DEFG的面积是$\frac{144}{49}$. △ABC中,AB=9,∠B=2∠C,AD⊥BC,AE是BC边上中线,则线段DE=4.5.
△ABC中,AB=9,∠B=2∠C,AD⊥BC,AE是BC边上中线,则线段DE=4.5.