题目内容
4．
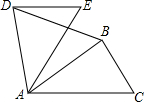如图，如果△ABC绕点A逆时针方向旋转60°后得到△ADE，且AB=2，那么BD的长为（ ）| A． | 1 | B． | 2 | C． | 2$\sqrt{3}$ | D． | 4 |
分析 根据旋转的性质，可得AD的长，根据等边三角形的判定，可得答案．
解答 解：由△ABC绕点A逆时针方向旋转60°后得到△ADE，得
AD=AB=2，∠BAD=60°．
△ABD是等边三角形，
BD=AB=2，
故选：B．
点评 本题考查了旋转的性质，利用旋转的性质得出△ABD是等边三角形是解题关键．
练习册系列答案
相关题目
18．若直线y=x+b与y=2x-a的交点为（k，3），则2b+a的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 无法计算 |
9．已知点D与点A（0，6），B（0，-4），C（x，y）是平行四边形的四个顶点，其中x，y满足3x-4y+12=0，则CD长的最小值为（ ）
| A． | 10 | B． | 2$\sqrt{7}$ | C． | $\frac{16}{5}$ | D． | 4 |
如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′•OP=r2，则称点P′是点P关于⊙O的“美好点”．如图2，⊙O的半径为2，点B在⊙O上，∠BOA=60°，OA=4，若点A′、B′分别是点A，B关于⊙O的美好点，求A′B′的长．
14．一元二次方程x2-x+4=0的根的情况为（ ）
| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 只有一个实数根 | D． | 没有实数根 |