题目内容
18. △ABC中,AB=9,∠B=2∠C,AD⊥BC,AE是BC边上中线,则线段DE=4.5.
△ABC中,AB=9,∠B=2∠C,AD⊥BC,AE是BC边上中线,则线段DE=4.5.
分析 首先过E点作ME∥AD,交AC于M,连接BM,易证得△MAB∽△BAC,又由ME∥AD,根据比例线段的性质,即可求得AB=2DE,继而求得答案.
解答 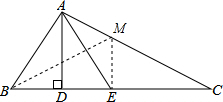 解:过E点作ME∥AD,交AC于M,连接BM,
解:过E点作ME∥AD,交AC于M,连接BM,
∴AD⊥BC,
∴ME⊥BC,
∵AE是BC边上中线,
∴BM=CM,
∴∠C=∠CBM,
又∵∠B=2∠C,
∴∠MBA=∠C,
又∵∠CAB=∠CAB,
∴△MAB∽△BAC,
∴$\frac{AB}{AM}$=$\frac{BC}{BM}$=$\frac{BC}{CM}$.
∵ME∥AD,
∴$\frac{CE}{CM}$=$\frac{DE}{AM}$,
∵CE=$\frac{1}{2}$CB,
∴$\frac{BC}{CM}$=$\frac{2DE}{AM}$,
∴$\frac{AB}{AM}$=$\frac{2DE}{AM}$,
∴AB=2DE,
∵AB=9,
∴DE=4.5.
故答案为:4.5.
点评 此题考查了相似三角形的判定与性质、等腰三角形的判定与性质以及平行线分线段成比例定理.注意正确的作出辅助线是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
9.已知点D与点A(0,6),B(0,-4),C(x,y)是平行四边形的四个顶点,其中x,y满足3x-4y+12=0,则CD长的最小值为( )
| A. | 10 | B. | 2$\sqrt{7}$ | C. | $\frac{16}{5}$ | D. | 4 |
3.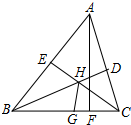 如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
 如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.一轮船从A地到B地需7天,而从B地到A地只需5天,则一竹排从B地漂到A地需要的天数是( )
| A. | 12 | B. | 35 | C. | 24 | D. | 47 |
7.不解方程,判断方程2x2-4x-1=0的根的情况( )
| A. | 没有实数根 | B. | 有两个相等实数根 | ||
| C. | 有两个不相等实数根 | D. | 无法确定 |
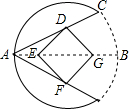 如图,在圆的正中央摆放着一个正方形DEFG,且正方形的顶点D在弦AC上、对角线EG在直径AB上.若EG=4,AB=8,则AC=$\frac{16\sqrt{5}}{5}$.
如图,在圆的正中央摆放着一个正方形DEFG,且正方形的顶点D在弦AC上、对角线EG在直径AB上.若EG=4,AB=8,则AC=$\frac{16\sqrt{5}}{5}$. 如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“美好点”.如图2,⊙O的半径为2,点B在⊙O上,∠BOA=60°,OA=4,若点A′、B′分别是点A,B关于⊙O的美好点,求A′B′的长.
如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“美好点”.如图2,⊙O的半径为2,点B在⊙O上,∠BOA=60°,OA=4,若点A′、B′分别是点A,B关于⊙O的美好点,求A′B′的长.