题目内容
15.解下列方程:(1)x2-2$\sqrt{3}$x+3=0
(2)x2-3x+2=0
(3)3(x-2)2=x(x-2)
(4)x2-5x+1=0(用配方法).
分析 (1)利用完全平方公式因式分解求得方程的解;
(2)(3)利用因式分解法求得方程的解;
(4)利用配方法解方程.
解答 解:(1)x2-2$\sqrt{3}$x+3=0
(x-$\sqrt{3}$)2=0
解得:x1=x2=$\sqrt{3}$;
(2)x2-3x+2=0
(x-1)(x-2)=0
x-1=0,x-2=0
解得:x1=2,x2=1;
(3)3(x-2)2=x(x-2)
(x-2)[3(x-2)-x]=0
(x-2)(2x-6)=0
解得:x1=2,x2=3;
(4)x2-5x+1=0
x2-5x=-1
x-5x+$\frac{25}{4}$=$\frac{21}{4}$
(x-$\frac{5}{2}$)2=$\frac{21}{4}$
x-$\frac{5}{2}$=±$\frac{\sqrt{21}}{2}$
解得:x1=$\frac{5+\sqrt{21}}{2}$,x2=$\frac{5-\sqrt{21}}{2}$.
点评 本题考查了解一元二次方程--因式分解法、直接开平方法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
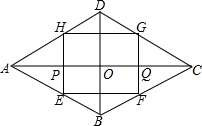 如图,在菱形ABCD中,两条对角线长是AC=10,BD=6,F是线段AO上一点(不与A、O重合),Q是线段OC上一点,且AP=CQ,分别将∠BAD和∠BCD折叠,使A、C两点都在对角线AC上,折痕分别是EH和FG,EH过P点,FG过Q点,连接EF、HG,再把折叠部分铺平.
如图,在菱形ABCD中,两条对角线长是AC=10,BD=6,F是线段AO上一点(不与A、O重合),Q是线段OC上一点,且AP=CQ,分别将∠BAD和∠BCD折叠,使A、C两点都在对角线AC上,折痕分别是EH和FG,EH过P点,FG过Q点,连接EF、HG,再把折叠部分铺平. 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.