题目内容
16.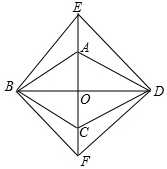 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.(1)求证:△BAE≌△BCF;
(2)若∠ABC=40°,则当∠EBA=25°时,四边形BFDE是正方形.
分析 (1)由菱形的性质得出AB=CB,由等腰三角形的性质得出∠BAC=∠BCA,证出∠BAE=∠BCF,由SAS证明△BAE≌△BCF即可;
(2)由菱形的性质得出AC⊥BD,OA=OC,OB=OD,∠ABO=$\frac{1}{2}$∠ABC=20°,证出OE=OF,得出四边形BFDE是菱形,证明△OBE是等腰直角三角形,得出OB=OE,BD=EF,证出四边形BFDE是矩形,即可得出结论.
解答 (1)证明:∵四边形ABCD是菱形,
∴AB=CB,
∴∠BAC=∠BCA,
∴180°-∠BAC=180°-∠BCA,
即∠BAE=∠BCF,
在△BAE和△BCF中,$\left\{\begin{array}{l}{AB=CB}&{\;}\\{∠BAE=∠BCF}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△BAE≌△BCF(SAS);
(2)解:若∠ABC=40°,则当∠EBA=25°时,四边形BFDE是正方形.理由如下:
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠ABO=$\frac{1}{2}$∠ABC=20°,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
又∵AC⊥BD,∴四边形BFDE是菱形,
∵∠EBA=25°,
∴∠OBE=25°+20°=45°,
∴△OBE是等腰直角三角形,
∴OB=OE,
∴BD=EF,
∴四边形BFDE是矩形,
∴四边形BFDE是正方形;
故答案为:25.
点评 本题考查了正方形的判定、全等三角形的判定与性质、菱形的判定与性质、矩形的判定;熟练掌握全等三角形的判定与性质和菱形的判定与性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
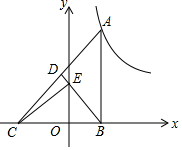 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$\sqrt{6}$,则k的值为2$\sqrt{6}$.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$\sqrt{6}$,则k的值为2$\sqrt{6}$. 如图,EB∥DC,∠C=∠E,∠A和∠ADE有何关系?并说明你的理由.
如图,EB∥DC,∠C=∠E,∠A和∠ADE有何关系?并说明你的理由. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=66°,则∠AED′的度数为48°.
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=66°,则∠AED′的度数为48°. 如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°.
如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°.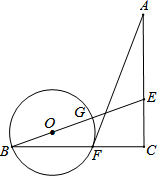 如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,且CE=CF.连结AF和BE上,⊙O经过点B、F.
如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,且CE=CF.连结AF和BE上,⊙O经过点B、F.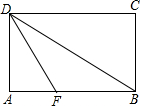 如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在BD的中点处,则∠ADF=30°.
如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在BD的中点处,则∠ADF=30°. 如图,O是矩形ABCD对角线的交点,BO=BE,∠AOD=120°,∠AEO=30°.
如图,O是矩形ABCD对角线的交点,BO=BE,∠AOD=120°,∠AEO=30°.