题目内容
6.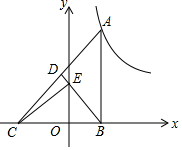 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$\sqrt{6}$,则k的值为2$\sqrt{6}$.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$\sqrt{6}$,则k的值为2$\sqrt{6}$.
分析 作AF⊥y轴于F,EH⊥AB于H,由于BD为斜边AC上的中线,根据三角形面积公式得到S△ABE=S△CBE=$\sqrt{6}$,再利用矩形的面积公式得到S矩形ABOF=2S△ABE=2$\sqrt{6}$,然后根据反比例函数y=$\frac{k}{x}$(k≠0)中比例系数k的几何意义即可得到k的值.
解答 解:作AF⊥y轴于F,EH⊥AB于H,如图,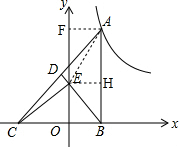
∵BD为斜边AC上的中线,
∴S△ABE=S△CBE=$\sqrt{6}$,
∴S矩形ABOF=2S△ABE=2$\sqrt{6}$,
∴k=2$\sqrt{6}$.
故答案为2$\sqrt{6}$.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.

练习册系列答案
相关题目
2.计算:(-$\frac{1}{2}$)2-1=( )
| A. | -$\frac{5}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | 0 |
11.下列各式中无论x为任何数都没有意义的是( )
| A. | $\sqrt{-7x}$ | B. | $\sqrt{-199{9x}^{3}}$ | C. | $\sqrt{{-0.1x}^{2}-1}$ | D. | $\root{3}{-{6x}^{2}-5}$ |

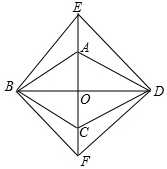 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.