题目内容
17.在平面直角坐标系中,点A(-4,0),点B(2,0),若点C在一次函数y=-$\frac{1}{2}x+2$的图象上,且△ABC为直角三角形,则满足条件的点C有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据已知可求得直线与两轴的交点,①分别过点A、点B作垂线,可得出符合题意的点C,②利用圆周角定理,可得出符合条件的两个点C.
解答 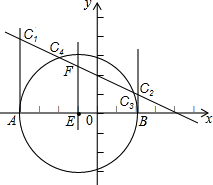 解:由题意知,直线y=-$\frac{1}{2}$x+2与x轴的交点为(4,0),与y轴的交点为(0,2),如图:
解:由题意知,直线y=-$\frac{1}{2}$x+2与x轴的交点为(4,0),与y轴的交点为(0,2),如图:
当∠A=90°时,
过点A作垂线与直线的交点C1(-4,4);
当∠B=90°时,过点B作垂线与直线的交点C2(2,1);
当∠C=90°时,
过AB中点E(-1,0),作垂线与直线的交点为F(-1,2.5),则EF=2.5<3,
所以以3为半径,以点E为圆心的圆与直线必有两个交点,
设C3(x,-$\frac{1}{2}$x+2),
则AC2+BC2=AB2,即(x+4)2+2(-$\frac{1}{2}$x+2)2+(x-2)2=36,解得x=±$\frac{4\sqrt{5}}{5}$,
当x=$\frac{4\sqrt{5}}{5}$时,y=-$\frac{2\sqrt{5}}{5}$+10;
当x=-$\frac{4\sqrt{5}}{5}$时,y=$\frac{2\sqrt{5}}{5}$+10.
故C3($\frac{4\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$+10),C4(-$\frac{4\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$+10).
综上所述,点C的坐标为:C1(-4,4),C2(2,1),C3($\frac{4\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$+10),C4(-$\frac{4\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$+10).
故选C.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 若ab=0,则点P(a,b)表示原点 | B. | 坐标轴上的点不属于任何象限 | ||
| C. | 已知点A(3,-2),则它到x轴的距离为3 | D. | 点(1,-a2)在第四象限 |
 如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )
如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )| A. | -4 | B. | 2 | C. | 4 | D. | 3 |
| A. | (-5,3) | B. | (3,-5) | C. | (-3,5) | D. | (5,-3) |
| A. | (42,15) | B. | (1,4) | C. | (15,42) | D. | (15,4) |
| A. | (2,5) | B. | (-6,-1) | C. | (-8,-3) | D. | (-2,-2) |
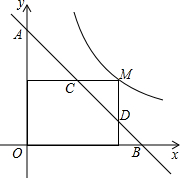 如图,M为双曲线y=$\frac{2}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为4.
如图,M为双曲线y=$\frac{2}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为4.