题目内容
20.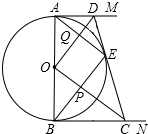 如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:①⊙O的半径为$\frac{13}{2}$;②OD∥BE; ③PB=$\frac{18}{13}$$\sqrt{13}$;④tan∠CEP=$\frac{2}{3}$.
其中正确结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 作DK⊥BC于K,连接OE,①错误,在Rt△CDK中,利用勾股定理求得DK=12,故错误.②正确.可以证明AQ=QE,AO=OB,由此得出结论.③正确.根据PB=$\frac{BC•OB}{OC}$计算即可.④错误;根据tan∠CEP=tan∠CBP=$\frac{PC}{PB}$计算即可.
解答 解: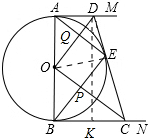 作DK⊥BC于K,连接OE.
作DK⊥BC于K,连接OE.
∵AD、BC是切线,
∴∠DAB=∠ABK=∠DKB=90°,
∴四边形ABKD是矩形,
∴DK=AB,AD=BK=4,
∵CD是切线,
∴DA=DE,CE=CB=9,
在Rt△DKC中,∵DC=DE+CE=13,CK=BC-BK=5,
∴DK=$\sqrt{D{C}^{2}-C{K}^{2}}$=12,
∴AB=DK=12,
∴⊙O半径为6.故①错误,
∵DA=DE,OA=OE,
∴OD垂直平分AE,同理OC垂直平分BE,
∴AQ=QE,∵AO=OB,
∴OD∥BE,故②正确.
在Rt△OBC中,PB=$\frac{OB•BC}{OC}$=$\frac{6×9}{3\sqrt{13}}$=$\frac{18\sqrt{13}}{13}$,故③正确,
∵CE=CB,
∴∠CEB=∠CBE,
∴tan∠CEP=tan∠CBP=$\frac{PC}{BP}$=$\frac{\frac{27\sqrt{13}}{13}}{\frac{18\sqrt{13}}{13}}$=$\frac{3}{2}$,故④错误,
∴②③正确,
故选B.
点评 本题考查切线的性质、圆周角定理、切线长定理、勾股定理、三角形中位线性质、直角三角形斜边上的高的求法等知识,解题的关键是添加辅助线构造直角三角形解决问题,熟练掌握切线长定理,属于中考常考题型.

练习册系列答案
相关题目
10.若等腰三角形的一边长为6,另两边长分别是关于x的方程x2-(k+5)x+3k+6=0的两个根,则k的值是( )
| A. | -1或4 | B. | -1 | C. | 1或4 | D. | 4 |
11.一次函数y=-x+4的图象与两坐标轴所围成的三角形的面积为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
8. 如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )
如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )
 如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )
如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )| A. | -4 | B. | 2 | C. | 4 | D. | 3 |
15. 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )| A. | 0.8πcm2 | B. | 3.2πcm2 | C. | 4πcm2 | D. | 4.8πcm2 |
5.点P在第二象限,且到x轴的距离为5,到y轴的距离为3,则点P的坐标是( )
| A. | (-5,3) | B. | (3,-5) | C. | (-3,5) | D. | (5,-3) |
12.一影院观众席中的9排23号记作(9,23),那么15排42号的位置应记作( )
| A. | (42,15) | B. | (1,4) | C. | (15,42) | D. | (15,4) |
10.对于一次函数y=-2x+4,下列结论错误的是( )
| A. | 函数值随自变量的增大而减小 | |
| B. | 当x<0时,y<4 | |
| C. | 函数的图象向下平移4个单位长度得y=-2x的图象 | |
| D. | 函数的图象与y轴的交点坐标是(0,4) |