题目内容
12.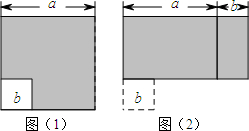 如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.
如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.(1)请你分别表示出这两个图形中阴影部分的面积:a2-b2、(a+b)(a-b).
(2)请问以上结果可以验证哪个乘法公式?a2-b2=(a+b)(a-b).
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1.
分析 (1)求出大正方形及小正方形的面积,作差即可得出阴影部分的面积,图(2)所示的长方形的长和宽分别为(a+b)、(a-b),由此可计算出面积;
(2)根据阴影部分的面积相等可得出平方差公式;
(3)利用原式补项(2-1),进而利用平方差公式求出答案.
解答 解:(1)∵大正方形的面积为a2,小正方形的面积为b2,
故图(1)阴影部分的面积值为:a2-b2,图(2)阴影部分的面积值为:(a+b)(a-b).
故答案为:a2-b2,(a+b)(a-b);
(2)以上结果可以验证乘法公式:a2-b2=(a+b)(a-b).
故答案为:a2-b2=(a+b)(a-b);
(3)原式=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1
=264-1+1
=264.
点评 本题考查了平方差公式的几何背景,注意几次分割后边的变化情况是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
7. 一只蚂蚁从A点沿着一个长方体框架的棱爬到B点,蚂蚁至少爬了( )cm.
一只蚂蚁从A点沿着一个长方体框架的棱爬到B点,蚂蚁至少爬了( )cm.
 一只蚂蚁从A点沿着一个长方体框架的棱爬到B点,蚂蚁至少爬了( )cm.
一只蚂蚁从A点沿着一个长方体框架的棱爬到B点,蚂蚁至少爬了( )cm.| A. | 12 | B. | 48 | C. | 60 | D. | 94 |
17.若(x+3)(x-2)=x2+mx+n,则m-n的值为( )
| A. | -1 | B. | 1 | C. | 5 | D. | 7 |
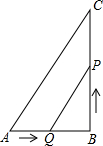 如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿 AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.
如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿 AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.