题目内容
2.计算:(1)计算:$-{3^2}+{(\frac{1}{2})^{-3}}+\sqrt{{{(\sqrt{2}-\sqrt{3})}^2}}$+2sin45°+($\frac{4}{2014-π}$)0.
(2)先化简,再求值:$(\frac{a-2}{{{a^2}+2a}}-\frac{a-1}{{{a^2}+4a+4}})÷\frac{a-4}{a+2}$,其中a=$\sqrt{2}-1$.
分析 (1)先计算负整数指数幂、零指数幂以及特殊角的三角形函数值,然后计算加减法;
(2)先化简括号内的分式,然后化除法为乘法进行化简,再代入求值.
解答 解:(1)原式=-9+8+$\sqrt{3}$-$\sqrt{2}$+2×$\frac{\sqrt{2}}{2}$+1=$\sqrt{3}$;
(2)原式={$\frac{a-2}{a(a-2)}$-$\frac{a-1}{(a+2)^{2}}$}÷$\frac{a-4}{a+2}$,
=$\frac{(a+2)(a-2)-a(a-1)}{a(a+2)^{2}}$×$\frac{a+2}{a-4}$,
=$\frac{1}{a(a+2)}$,
=$\frac{1}{{a}^{2}+2a}$.
∵a=$\sqrt{2}-1$,
∴a+1=a=$\sqrt{2}$,
∴a2+2a+1=2,
则a2+2a=1,
∴原式=1.
点评 本题考查了负整数指数幂、零指数幂、特殊角的三角形函数值以及分式的化简求值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
12.一年三班女生的人数是男生的$\frac{5}{6}$,如果男生有30人,那么一年三班共有( )
| A. | 25人 | B. | 5人 | C. | 55人 | D. | 50人 |
13.检查一个门框是矩形的方法是( )
| A. | 测量两条对角线是否相等 | B. | 测量有三个角是直角 | ||
| C. | 测量两条对角线是否互相平分 | D. | 测量两条对角线是否互相垂直 |
7.已知$\frac{x}{{{x^2}+x+1}}=\frac{1}{8}$(0<x<1).则$\sqrt{x}-\frac{1}{{\sqrt{x}}}$的值为( )
| A. | $-\sqrt{7}$ | B. | $\sqrt{7}$ | C. | $-\sqrt{5}$ | D. | $\sqrt{5}$ |
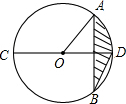 如图,CD是⊙O的直径,弦AB⊥CD,∠ABD=30°,若$CD=2\sqrt{6}$,则阴影部分图形的面积为π.
如图,CD是⊙O的直径,弦AB⊥CD,∠ABD=30°,若$CD=2\sqrt{6}$,则阴影部分图形的面积为π.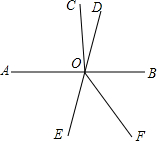 如图,已知直线AB和ED相交于点O(∠AOE为锐角),射线OC⊥AB于点O,OF平分∠BOE.
如图,已知直线AB和ED相交于点O(∠AOE为锐角),射线OC⊥AB于点O,OF平分∠BOE.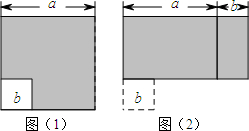 如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.
如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.