题目内容
4.已知△ABC≌△DEF,△ABC的三边长分别为4、m、n,△DEF的三边长分别为5、p、q.若△ABC的三边长均为整数,则m+n+p+q的最大值为25.分析 根据全等三角形对应边相等可得m、n中有一边为5,p、q有一边为4,剩下的两边相等,再根据三角形的任意两边之和大于第三边求出最长的边,然后相加即可.
解答 解:∵△ABC≌△DEF,
∴m、n中有一边为5,
p、q中有一边为4,
m、n与p、q中剩余两边相等,
∵4+5=9,
∴两三角形剩余两边最大为8,
∴m+n+p+q的最大值为:4+5+8+8=25.
故答案为:25
点评 本题考查了全等三角形对应边相等的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
15.下列各组整式中,不是同类项的是( )
| A. | -7与2.1 | B. | 2xy与-5yx | C. | a2b与ab2 | D. | mn2与3n2m |
19.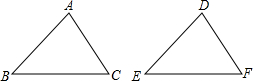 如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
 如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )| A. | BC=EF | B. | AB=DF | C. | AC=DE | D. | ∠A=∠D |
9.在Rt△ABC中,∠C=90°,∠B=30°,AC=4,AB=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
16.若a为方程x2+2x-5=0的解,则3a2+6a+1的值为( )
| A. | 12 | B. | 16 | C. | 9 | D. | 6 |
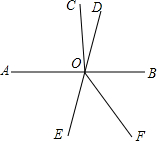 如图,已知直线AB和ED相交于点O(∠AOE为锐角),射线OC⊥AB于点O,OF平分∠BOE.
如图,已知直线AB和ED相交于点O(∠AOE为锐角),射线OC⊥AB于点O,OF平分∠BOE.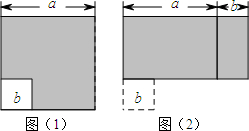 如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.
如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形. 如图,一菜农要修建一个育苗棚,棚宽BE=2m,棚高AE=1.5m,长BC=18m.AE所在的墙面与地面垂直,现要在棚顶覆盖一种农用塑料薄膜,请你为他计算一下,共需多少这种塑料薄膜45m2.
如图,一菜农要修建一个育苗棚,棚宽BE=2m,棚高AE=1.5m,长BC=18m.AE所在的墙面与地面垂直,现要在棚顶覆盖一种农用塑料薄膜,请你为他计算一下,共需多少这种塑料薄膜45m2. 如图,公路PQ和公路MN交于点P,且∠NPQ=30°,公路PQ上有一所学校A,AP=160米.若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响,假设拖拉机行驶时周围100米以内会受到噪声的影响;则造成影响的时间为$\frac{20}{3}$秒.
如图,公路PQ和公路MN交于点P,且∠NPQ=30°,公路PQ上有一所学校A,AP=160米.若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响,假设拖拉机行驶时周围100米以内会受到噪声的影响;则造成影响的时间为$\frac{20}{3}$秒.