题目内容
18.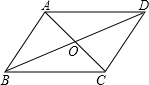 如图,?ABCD的对角线AC、BD交于点O.
如图,?ABCD的对角线AC、BD交于点O.(1)图中共有多少对全等的三角形?请把它们都写出来;
(2)选出其中一对:△ABO≌△CDO,给予证明.证明:
分析 (1)直接利用平行四边形的性质结合全等三角形的判定方法得出即可;
(2)利用全等三角形的判定方法得出即可.
解答 解:(1)图中共有4对全等的三角形,分别是:△ABO≌△CDO,△ADO≌△CBO,△ABC≌△CDA,△ABD≌△CDB;
(2)∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠ABD=∠CDB,
在△ABO和△CDO中,
$\left\{\begin{array}{l}{∠AOB=∠COD}\\{∠ABO=∠CDO}\\{AB=DC}\end{array}\right.$,
∴△ABO≌△CDO(AAS).
点评 此题主要考查了全等三角形的判定以及平行四边形的性质,熟练应用平行四边形的性质是解题关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
3.对于函数y=$\frac{6}{x}$,下列说法错误的是( )
| A. | 它的图象分布在第一、三象限 | B. | 当x>0时,y的值随x的增大而增大 | ||
| C. | 它的图象与直线y=-x无交点 | D. | 当x<0时,y的值随x的增大而减小 |
10.已知$\frac{x-y}{x+y}=3$,则代数式$\frac{x-y}{x+y}+$$\frac{3(x+y)}{x-y}+$$\frac{7}{2}$的值为( )
| A. | 8 | B. | 7 | C. | $\frac{15}{2}$ | D. | 6 |
7.直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),则不等式x2+bx+c>x+m的解集为( )
| A. | 0<x<2 | B. | x<2 | C. | 0<x<3 | D. | x<1或x>3 |
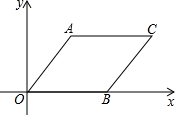 如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为20,点B的坐标是(5,0).
如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为20,点B的坐标是(5,0).