题目内容
3.对于函数y=$\frac{6}{x}$,下列说法错误的是( )| A. | 它的图象分布在第一、三象限 | B. | 当x>0时,y的值随x的增大而增大 | ||
| C. | 它的图象与直线y=-x无交点 | D. | 当x<0时,y的值随x的增大而减小 |
分析 根据反比例函数的性质对四个选项进行逐一分析即可.
解答 解:A、∵函数y=$\frac{6}{x}$中k=6>0,∴此函数图象的两个分支分别在一、三象限,故本选项正确;
B、∵当x>0时,函数的图象在第一象限,∴y的值随x的增大而减小,故本选项错误;
C、∵函数y=-x位于二、四象限,∴与反比例函数y=$\frac{6}{x}$无交点,故本选项正确;
D、∵当x<0时,函数的图象在第三象限,∴y的值随x的增大而减小,故本选项正确.
故选B.
点评 本题考查的是反比例函数的性质,即反比例函数y=xk(k≠0)的图象是双曲线,当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.在-5,-9,-3.5,-0.01,-2,-212各数中,最大的数是( )
| A. | -12 | B. | -9 | C. | -0.01 | D. | -5 |
13.下列说法中正确的是( )
| A. | 在数轴上与原点距离越远的点表示的数越大 | |
| B. | 在数轴上-9与-7中间的有理数是-8 | |
| C. | 所有的有理数都能在数轴上找到唯一对应的一点表示 | |
| D. | 数轴上每一点都表示有理数 |
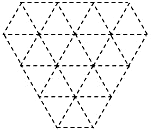 根据题意作出图形,并回答相关问题:请在网格中设计一个图案(图中每个小三角形都是边长为 1的等边三角形),要求所设计的图案既是轴对称图形,又是中心对称图形,并且图案的顶点在格点上,面积等于3$\sqrt{3}$.请将你所设计的图案用铅笔涂黑.
根据题意作出图形,并回答相关问题:请在网格中设计一个图案(图中每个小三角形都是边长为 1的等边三角形),要求所设计的图案既是轴对称图形,又是中心对称图形,并且图案的顶点在格点上,面积等于3$\sqrt{3}$.请将你所设计的图案用铅笔涂黑.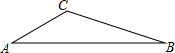 在△ABC中,∠A=30,tanB=$\frac{1}{3}$,BC=$\sqrt{10}$.求AB的长.
在△ABC中,∠A=30,tanB=$\frac{1}{3}$,BC=$\sqrt{10}$.求AB的长.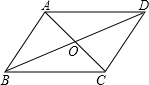 如图,?ABCD的对角线AC、BD交于点O.
如图,?ABCD的对角线AC、BD交于点O.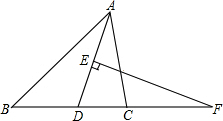 如图,在△ABC中,FD2=FB•FC,AD的垂直平分线交AD于E,交BC的延长线于F,求证:AD平分∠BAC.
如图,在△ABC中,FD2=FB•FC,AD的垂直平分线交AD于E,交BC的延长线于F,求证:AD平分∠BAC. 如图,在平面直角坐标系xOy中,抛物线y=x2+mx+n经过点A(0,-1),B(3,2)
如图,在平面直角坐标系xOy中,抛物线y=x2+mx+n经过点A(0,-1),B(3,2)