题目内容
6.如图,△ABC是学生小强家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在A的南偏东30°方向上,点C在A的南偏西75°的方向上,点C在B的北偏西75°的方向上,AC间距离为200米.问小强沿三角形绿化区的周边小路跑两圈共跑了多少米?(结果保留整数.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)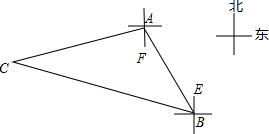
分析 过点A作AD⊥BC交BC于一点D,根据题意得∠FAE=30°,∠CBE=75°,利用三角形的外角的性质得到∠C=180°-75°-30°-45°=30°,然后在Rt△ADB中,求得AD=100米,CD=$100\sqrt{3}$米后即可求得三角形ABC的周长.
解答 解:过点A作AD⊥BC交BC于一点D,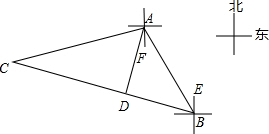
根据题意得∠FAE=30°,∠CBE=75°,
故∠ABE=∠FAE=30°,
∴∠ABC=45°,
∴∠DAB=∠ABC=45°,
∴∠C=180°-75°-30°-45°=30°,
在Rt△ADC中,
∵AC=200米,∠C=30°,
∴AD=100米,CD=$100\sqrt{3}$米
在Rt△ADB中,
∵AD=00米,∠ABC=45°,
∴AB=100$\sqrt{2}$米,DB=100米
∴BC=CD+DB=(100+100$\sqrt{3}$)米,
∴三角形ABC的周长为200+100$\sqrt{3}$+100+100$\sqrt{2}$≈615米
沿三角形绿化区的周边小路跑两圈共跑了约1230米.
点评 本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形模型并求解.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
14.在-5,-9,-3.5,-0.01,-2,-212各数中,最大的数是( )
| A. | -12 | B. | -9 | C. | -0.01 | D. | -5 |
1.在发生“甲型H7N9禽流感”疫情期间,有专业机构认为在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
| A. | 甲地:总体平均数为3,中位数为4 | |
| B. | 乙地:中位数为2,众数为3 | |
| C. | 丙地:总体平均数为2,总体方差为3 | |
| D. | 丁地:总体平均数为1,总体方差大于0 |
 已知:如图,平行四边形ABCD中,对角线AC的垂直平分线交AD于点E,交BC于点F,求证:四边形AFCE是菱形.
已知:如图,平行四边形ABCD中,对角线AC的垂直平分线交AD于点E,交BC于点F,求证:四边形AFCE是菱形. 在△ABC中,∠A=30,tanB=$\frac{1}{3}$,BC=$\sqrt{10}$.求AB的长.
在△ABC中,∠A=30,tanB=$\frac{1}{3}$,BC=$\sqrt{10}$.求AB的长.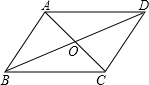 如图,?ABCD的对角线AC、BD交于点O.
如图,?ABCD的对角线AC、BD交于点O.