题目内容
8.某足球队的庆功晚宴上,出席者两两碰杯一次,共碰杯820次,则出席晚宴的有41人.分析 利用基本数量关系:两两碰杯一次,总次数为 $\frac{1}{2}$n(n-1)(n表示人数)列方程解答即可.
解答 解:设有x人参加了这次宴会,根据题意列方程得,
$\frac{1}{2}$x(x-1)=820,
解得:x1=41,x2=-40(不符合题意,舍去).
故答案为:41.
点评 此题考查一元二次方程的应用中的基本数量关系:单循环比赛进行的总场数为:$\frac{1}{2}$n(n-1),依此数量关系推广到一般问题.

练习册系列答案
相关题目
3.式子$\sqrt{x-2}$•$\sqrt{x+1}$=$\sqrt{(x-2)(x+1)}$成立的条件是( )
| A. | x≤2 | B. | x≥2 | C. | x≥-1 | D. | -1≤x≤2 |
13.下列说法中正确的是( )
| A. | 在数轴上与原点距离越远的点表示的数越大 | |
| B. | 在数轴上-9与-7中间的有理数是-8 | |
| C. | 所有的有理数都能在数轴上找到唯一对应的一点表示 | |
| D. | 数轴上每一点都表示有理数 |
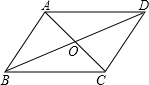 如图,?ABCD的对角线AC、BD交于点O.
如图,?ABCD的对角线AC、BD交于点O.