题目内容
9.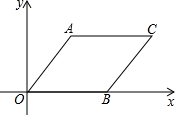 如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为20,点B的坐标是(5,0).
如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为20,点B的坐标是(5,0).
分析 过A作AE⊥x轴于点E,根据勾股定理可求出OA的长,进而可求出菱形的周长,再由菱形的性质可得AO=AC=BO=BC=5,即可求出点B的坐标.
解答 解:过A作AE⊥x轴于点E,
∵点A的坐标是(3,4),
∴OE=3,AE=4.
∴AO=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵四边形AOBC是菱形,
∴AO=AC=BO=BC=5,
∴菱形的周长=4AB=20,点B的坐标是(5,0),
故答案为:20,(5,0).
点评 此题主要考查了菱形的性质,解题的关键是利用勾股定理求出OA的长,是中考常见题型,比较简单.

练习册系列答案
相关题目
19.(-8)2014+(-8)2013能被下列数整除的是( )
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
14.在-5,-9,-3.5,-0.01,-2,-212各数中,最大的数是( )
| A. | -12 | B. | -9 | C. | -0.01 | D. | -5 |
1.在发生“甲型H7N9禽流感”疫情期间,有专业机构认为在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
| A. | 甲地:总体平均数为3,中位数为4 | |
| B. | 乙地:中位数为2,众数为3 | |
| C. | 丙地:总体平均数为2,总体方差为3 | |
| D. | 丁地:总体平均数为1,总体方差大于0 |
 已知:如图,平行四边形ABCD中,对角线AC的垂直平分线交AD于点E,交BC于点F,求证:四边形AFCE是菱形.
已知:如图,平行四边形ABCD中,对角线AC的垂直平分线交AD于点E,交BC于点F,求证:四边形AFCE是菱形.
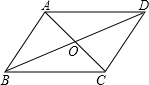 如图,?ABCD的对角线AC、BD交于点O.
如图,?ABCD的对角线AC、BD交于点O.