题目内容
8.已知:抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,抛物线的对称轴交x轴于点E,点A的坐标为(-1,0),点B的坐标为(3,0).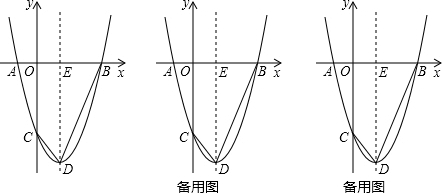
(1)求抛物线的解析式;
(2)连接BC,求△BCD的面积;
(3)在对称轴右侧的抛物线上有一点P,过点P作PK⊥直线CD,垂足为K,使∠CPK=∠BDE,求点P的坐标.
分析 (1)将点A、B的坐标代入抛物线表达式,然后解方程组求出b、c的值即可;
(2)连接BC,设直线BC与对称轴相交于点F,求出直线BC的解析式,根据抛物线解析式求出点D的坐标,再求出DF,然后根据三角形的面积公式列式计算即可得解;
(3)作出图形,根据点B、C、D的坐标求出BC⊥CD,再根据同角的余角相等求出∠BCP=∠CPK,从而得到的∠BCP=∠BDE,过点B作BG⊥BC交CP的延长线于G,过点G作GH⊥x轴于H,利用勾股定理列式求出BC,再求出△BCG和△EDB,然后根据相似三角形对应边成比例列式求出BG,根据平角等于180°求出∠GBH=45°,然后求出BH、GH,写出点G的坐标,再利用待定系数法求一次函数解析式求出直线CG的解析式,最后与抛物线解析式联立求解即可得到点P的坐标.
解答 解:(1)将A(-1,0),B(3,0)代入y=x2+bx+c得,
$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
所以,抛物线解析式为y=x2-2x-3;
(2)连接BC,设直线BC与对称轴相交于点F,
令x=0,则y=-3,
所以,点C(0,-3),
易求直线BC的解析式为y=x-3,
∵y=x2-2x-3=(x-1)2-4,
∴抛物线对称轴为直线x=1,顶点D的坐标为(1,-4),
当x=1时,y=1-3=-2,
∴点F(1,-2),
所以,DF=-2-(-4)=-2+4=2,
∴△BCD的面积=$\frac{1}{2}$×DF×3=$\frac{1}{2}$×2×3=3;
(3)如图,∵B(3,0),C(0,-3),D(1,-4),
∴BC、CD与y轴的夹角都是45°,
∴BC⊥CD,
∴∠BCP+∠PCK=90°,
∵PK⊥直线CD,
∴∠CPK+∠PCK=90°,
∴∠CPK=∠BCP,
∴∠CPK=∠BCP,
∵∠CPK=∠BDE,
∴∠BCP=∠BDE,
过点B作BG⊥BC交CP的延长线于G,过点G作GH⊥x轴于H,
由勾股定理列得,BC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
易求△BCG∽△EDB,
∴$\frac{BG}{BC}$=$\frac{BE}{DE}$,
即$\frac{BG}{3\sqrt{2}}$=$\frac{3-1}{4}$,
解得BG=$\frac{3\sqrt{2}}{2}$,
∵∠OBC=45°,
∴∠GBH=180°-45°-90°=45°,
∴BH=GH=$\frac{\sqrt{2}}{2}$BG=$\frac{\sqrt{2}}{2}$×$\frac{3\sqrt{2}}{2}$=$\frac{3}{2}$,
∴OH=OB+BH=3+$\frac{3}{2}$=$\frac{9}{2}$,
∴点G的坐标为($\frac{9}{2}$,-$\frac{3}{2}$),
设直线CG的解析式为y=kx+b,
则$\left\{\begin{array}{l}{\frac{9}{2}k+b=-\frac{3}{2}}\\{b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=-3}\end{array}\right.$,
所以,直线CG的解析式为y=$\frac{1}{3}$x-3,
联立$\left\{\begin{array}{l}{y={x}^{2}-2x-3}\\{y=\frac{1}{3}x-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=-3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{7}{3}}\\{{y}_{2}=-\frac{20}{9}}\end{array}\right.$,
所以,点P的坐标为($\frac{7}{3}$,-$\frac{22}{9}$).
点评 本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,三角形的面积,相似三角形的判定与性质,联立两函数解析式求交点坐标,难点在于(3)作辅助线构造出相似三角形并求出直线CP上的一个点的坐标.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 今年8月,我省大部分地区出现强降雨天气,洪水时刻威胁着人民的生命财产安全.下面是小明对某一水库的观测记录,他取警戒水位为0米,该水库一周内的水位变化情况如下:(测量前一天的水位达到了警戒水位,单位:米)
今年8月,我省大部分地区出现强降雨天气,洪水时刻威胁着人民的生命财产安全.下面是小明对某一水库的观测记录,他取警戒水位为0米,该水库一周内的水位变化情况如下:(测量前一天的水位达到了警戒水位,单位:米)| 时间 | 8月5日 | 8月6日 | 8月7日 | 8月8日 | 8月9日 | 8月10日 | 8月11日 |
| 水位变化/米 | +0.15 | -0.2 | +0.13 | -0.1 | +0.14 | -0.25 | +0.16 |
(1)这周内,哪一天的水位最高,哪一天的水位最低?它们是位于警戒水位之上还是之下,与警戒水位的距离分别是多少?
(2)与测量前一天比,一周内水库的水位是上升了,还是下降了?
(3)以警戒水位为0点,用折线统计图表示这一周水位的变化情况.(在坐标纸里画图)
| A. | 小于4cm | B. | 等于4cm | C. | 大于4cm | D. | 不确定 |
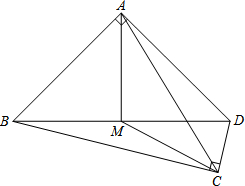 已知,如图,四边形ABCD中,∠BAD=∠BCD=90°,M为BD的中点,AB=AD,BD=$2\sqrt{17}$,CD=2.
已知,如图,四边形ABCD中,∠BAD=∠BCD=90°,M为BD的中点,AB=AD,BD=$2\sqrt{17}$,CD=2. 如图,一个六边形的六个内角都是120°,AB=1,BC=CD=3,DE=2,求该六边形的周长.
如图,一个六边形的六个内角都是120°,AB=1,BC=CD=3,DE=2,求该六边形的周长.