题目内容
13.求下列函数的自变量的取值范围.(1)y=2x+1;
(2)y=$\frac{1}{x-1}$;
(3)y=$\sqrt{x-5}$;
(4)y=-$\frac{1}{{x}^{2}}$.
分析 (1)由于函数表达式是整式,所以自变量可取全体实数;
(2)根据分式有意义的条件是分母不为0;分析原函数式可得关系式x-1≠0,解可得自变量x的取值范围;
(3)根据二次根式的意义被开方数是非负数;分析原函数式可得关系式x-5≥0,解可得自变量x的取值范围;
(4)根据分式有意义的条件是分母不为0;分析原函数式可得关系式x2≠0,解可得自变量x的取值范围.
解答 解:(1)y=2x+1,x是全体实数;
(2)y=$\frac{1}{x-1}$,分母不等于零,得x≠1;
(3)y=$\sqrt{x-5}$,被开方数是非负数,得x-5≥0,解得x≥5;
(4)y=-$\frac{1}{{x}^{2}}$分母不能等于零,得x≠0.
点评 本题考查了函数自变量的范围,当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
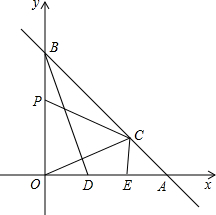 如图,直线L交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0
如图,直线L交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0