题目内容
3.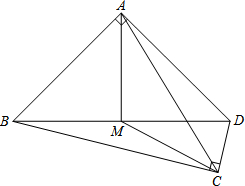 已知,如图,四边形ABCD中,∠BAD=∠BCD=90°,M为BD的中点,AB=AD,BD=$2\sqrt{17}$,CD=2.
已知,如图,四边形ABCD中,∠BAD=∠BCD=90°,M为BD的中点,AB=AD,BD=$2\sqrt{17}$,CD=2.(1)取AC中点E,连接ME,求证:ME⊥AC;
(2)在(1)的条件下,过点M作CD的垂线l,垂足为F,并交AC于点G,试说明:△MEG是等腰直角三角形.
分析 (1)由直角三角形斜边上的中线等于斜边的一半,得到AM=CM,根据三线合一得到结论;
(2))由∠AME+∠MAE=90°,得到∠EMD=∠MAE=∠MCE,由线段的中点得到MD=$\frac{1}{2}$BD,所以△DMC是等腰三角形,由三线合一得到MF⊥CD,∠DMF=∠CMF,于是∠EMG=∠EMD+∠DMF,∠EGM=∠MCE+∠CMF,推出∠EMG=∠EGM,由等角对等边得到EM=EG,又∠MEG=90°,得到△MEG是等腰直角三角形.
解答 解: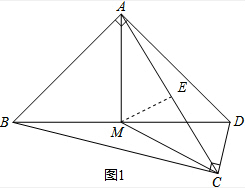 (1)∵∠BAD=∠BCD=90°,M是BD的中点,
(1)∵∠BAD=∠BCD=90°,M是BD的中点,
∴AM=$\frac{1}{2}$BD,CM=$\frac{1}{2}$BD,
∴AM=CM,
∵E是AC的中点,即ME是等腰三角形AMC的底边中线,
∴ME⊥AC,
∵AM=CM,
∴∠MAE=∠MCE,
∵AB=AD,AM是中线,
∴AM⊥BD,
∴∠AMD=90°,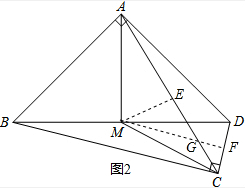
∴∠AME+∠EMD=90°,
∵ME⊥AC,
(2)∵∠AME+∠MAE=90°,
∴∠EMD=∠MAE=∠MCE,
∵CM=$\frac{1}{2}$BD=DM,
∵MF⊥CD,
∴∠DMF=∠CMF,
∵∠EMG=∠EMD+∠DMF,
∠EGM=∠MCE+∠CMF,
∴∠EMG=∠EGM,
∴EM=EG,
又∵∠MEG=90°,
∴△MEG是等腰直角三角形.
点评 本题考查了全等三角形的判定与性质,角平分线的性质,等腰三角形的判定与性质,直角三角形斜边的中线,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
 已知:平行四边形ABCD中,AB=2BC,延长CB到E,BE=BC,延长BC到F,CF=BC,AF、DE相交于G,求证:AF⊥DE.
已知:平行四边形ABCD中,AB=2BC,延长CB到E,BE=BC,延长BC到F,CF=BC,AF、DE相交于G,求证:AF⊥DE.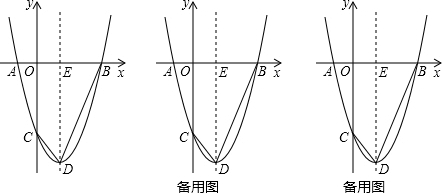

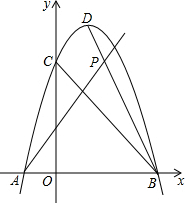 如图,已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B(点B在X轴的正半轴上),与y轴交于点C,其顶点为D,又tan∠OBC=1,过点A任作直线l交线段BD于点P,若点B、D到直线l的距离分别记为d1、d2,则d1+d2的最大值为$\sqrt{5}$.
如图,已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B(点B在X轴的正半轴上),与y轴交于点C,其顶点为D,又tan∠OBC=1,过点A任作直线l交线段BD于点P,若点B、D到直线l的距离分别记为d1、d2,则d1+d2的最大值为$\sqrt{5}$.