Question

小明是一个非常喜欢动脑筋肯钻研的同学，学习了特殊角的三角函数值后，他进行了如下探究：根据tan30°=

3

3

，构造Rt△ABC（如图所示），使∠BAC=30°，AB=2，BC=1，AC=

3

，再延长CA到点D，使AB=AD，连接BD，则∠D=15°，CD=2+

3

，因为在Rt△BCD中，tanD=

BC

CD

=

1

2+ 3

=2-

3

，故tan15°=2-

3

．
请你根据小明探究问题的思路，由tan45°=1，求出tan22.5°的值．

Answer 1

考点：解直角三角形

专题：阅读型

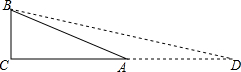
分析：构造Rt△ABC，使∠BAC=45°，AB=

2

AC=

2

BC，连接BD，则可知∠D=22.5°，在Rt△BDC中利用正切值的定义可求得答案．

解答：解：
如图，在Rt△ABC，使∠BAC=45°，AB=

2

，AC=BC=1，
延长CA到点D，使AB=AD，连接BD，则可知∠D=22.5°，且CD=CA+AD=1+

2

，
∵在Rt△BCD中，tan∠D=

BC

CD

=

1

1+ 2

=

2

-1，
∴tan22.5°=

2

-1．

点评：本题主要考查正切函数的定义，利用条件构造出22.5°的角是解题的关键．