题目内容
函数y=-3x+6的图象与x轴的交点坐标为 ,与y轴的交点坐标为 .与坐标轴围成的三角形为 .
考点:一次函数的图象
专题:
分析:直线与x轴交点的纵坐标为0,与y轴交点的横坐标为0,据此可以求得该直线与坐标轴的交点坐标,根据坐标轴互相垂直可以得到该三角形为直角三角形.
解答:解:令y=0,则-3x+6=0,解得 x=2,即函数y=-3x+6的图象与x轴的交点坐标为 (2,0),
令x=0,则y=6,即函数y=-3x+6的图象与y轴的交点坐标为 (0,6).
∵x轴⊥y轴,
∴函数y=-3x+6的图象与坐标轴围成的三角形为 直角三角形.
故答案是:(2,0);(0,6);直角三角形.
令x=0,则y=6,即函数y=-3x+6的图象与y轴的交点坐标为 (0,6).
∵x轴⊥y轴,
∴函数y=-3x+6的图象与坐标轴围成的三角形为 直角三角形.
故答案是:(2,0);(0,6);直角三角形.
点评:本题考查一次函数图象.解题的关键是掌握直线与坐标轴交点的坐标性质.

练习册系列答案
相关题目
若y=mx2+nx-p(其中m,n,p是常数)为二次函数,则( )
| A、m,n,p均不为0 |
| B、m≠0,且n≠0 |
| C、m≠0 |
| D、m≠0,或p≠0 |
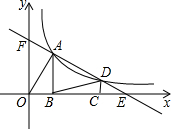 如图,点A,D是函数y=
如图,点A,D是函数y= 已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.
已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.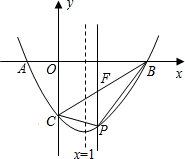 如图,在平面直角坐标系中,点A、C的坐标分别为(-1,0)、(0,-2),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1.
如图,在平面直角坐标系中,点A、C的坐标分别为(-1,0)、(0,-2),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1.