题目内容
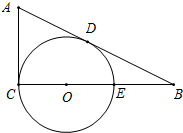 在△ABC中,∠ACB=90°,⊙O的圆心O在BC上,交BC于点C、E,且AB切⊙O于D,若OC:CB=1:3,AD=2,求BE.
在△ABC中,∠ACB=90°,⊙O的圆心O在BC上,交BC于点C、E,且AB切⊙O于D,若OC:CB=1:3,AD=2,求BE.考点:切线的性质,相似三角形的判定与性质
专题:
分析:利用切线的性质推知OD⊥AB,则利用“两角法”易证△BDO∽△BCA,利用该相似三角形的对应边成比例来求相关线段的长度.
解答: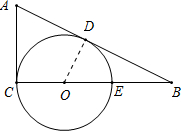 解:如图,连接OD.
解:如图,连接OD.
∵AB切⊙O于D,O是圆心,
∴OD⊥AB,
则∠ODB=90°,
又∠ACB=90°,
∴∠ODB=∠ACB=90°,AC=AD,
又∠B=∠B,
∴△BDO∽△BCA,
∴
=
=
∵OC:CB=1:3,OC=OE=OD,
∴OC=OE=BE=OD,
则
=
=
,
解得 BE=
.
 解:如图,连接OD.
解:如图,连接OD.∵AB切⊙O于D,O是圆心,
∴OD⊥AB,
则∠ODB=90°,
又∠ACB=90°,
∴∠ODB=∠ACB=90°,AC=AD,
又∠B=∠B,
∴△BDO∽△BCA,
∴
| BD |
| BC |
| OB |
| AB |
| OD |
| AC |
∵OC:CB=1:3,OC=OE=OD,
∴OC=OE=BE=OD,
则
| BD |
| 3BE |
| 2BE |
| 2+BD |
| BE |
| 2 |
解得 BE=
2
| ||
| 3 |
点评:本题考查了切线的性质和相似三角形的判定与性质.注意利用切线的性质推知AC=AD是通过比例式求得BE长度的关键.

练习册系列答案
相关题目
 如图,AB与⊙O切于点B,AO=5cm,AB=3cm,则⊙O的半径为( )
如图,AB与⊙O切于点B,AO=5cm,AB=3cm,则⊙O的半径为( )| A、4cm | ||
B、2
| ||
C、2
| ||
D、
|
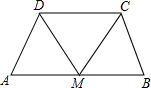 如图,点M是等腰梯形ABCD底边AB的中点,下列说法正确的是( )
如图,点M是等腰梯形ABCD底边AB的中点,下列说法正确的是( )| A、∠DAM=∠DCM |
| B、DM∥BC |
| C、△AMD≌△BMC |
| D、△AMD≌△DMC |
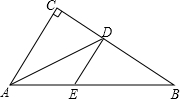 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE∥CA,CD=12,BD=15,求线段AE、BE的长.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE∥CA,CD=12,BD=15,求线段AE、BE的长. 现有长7m的材料,要制作如图的“目”字形的窗框,为使透过的光最大,则其中一边x应取何值?此时,窗框的面积为多少?
现有长7m的材料,要制作如图的“目”字形的窗框,为使透过的光最大,则其中一边x应取何值?此时,窗框的面积为多少?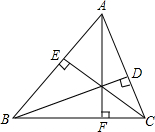 如图,已知AF、BD、CE为△ABC的高.求证:BC2=BE•AB+CD•AC.
如图,已知AF、BD、CE为△ABC的高.求证:BC2=BE•AB+CD•AC. 已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.
已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.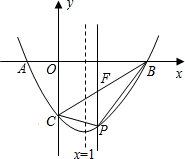 如图,在平面直角坐标系中,点A、C的坐标分别为(-1,0)、(0,-2),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1.
如图,在平面直角坐标系中,点A、C的坐标分别为(-1,0)、(0,-2),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1.