题目内容
已知圆锥的高为4,侧面展开图的圆心角为216°,求圆锥的全面积.
考点:圆锥的计算
专题:计算题
分析:设圆锥定的底面圆的半径为r,母线长为R,根据弧长公式得到2πr=
,解得r=
R,再利用勾股定理可计算出R与r,然后利用扇形面积公式求圆锥的侧面积和底面积.
| 216•π•R |
| 180 |
| 3 |
| 5 |
解答:解:设圆锥定的底面圆的半径为r,母线长为R,
根据题意得2πr=
,解得r=
R,
因为r2+42=R2,
所以(
R)2+42=R2,解得R=5,
所以r=3,
所以圆锥的全面积=π•32+
•2π•3•5=24π.
根据题意得2πr=
| 216•π•R |
| 180 |
| 3 |
| 5 |
因为r2+42=R2,
所以(
| 3 |
| 5 |
所以r=3,
所以圆锥的全面积=π•32+
| 1 |
| 2 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了勾股定理.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 a,b两数在数轴上的位置如图,下列结论正确的是( )
a,b两数在数轴上的位置如图,下列结论正确的是( )| A、a>0,b<0 |
| B、a<0,b>0 |
| C、ab>0 |
| D、以上都不对 |
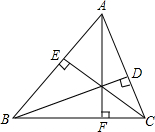 如图,已知AF、BD、CE为△ABC的高.求证:BC2=BE•AB+CD•AC.
如图,已知AF、BD、CE为△ABC的高.求证:BC2=BE•AB+CD•AC. 已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.
已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.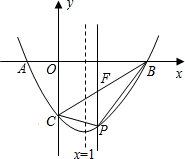 如图,在平面直角坐标系中,点A、C的坐标分别为(-1,0)、(0,-2),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1.
如图,在平面直角坐标系中,点A、C的坐标分别为(-1,0)、(0,-2),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1. 已知,如图,A,B分别为数轴上的两点,A点对应的数是-35,B点对应的数是85.
已知,如图,A,B分别为数轴上的两点,A点对应的数是-35,B点对应的数是85.