题目内容
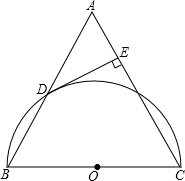 已知△ABC中,AB=AC,DE⊥AC于点E,DE与半⊙O相切于点D.
已知△ABC中,AB=AC,DE⊥AC于点E,DE与半⊙O相切于点D.求证:△ABC是等边三角形.
考点:切线的性质,等边三角形的判定
专题:证明题
分析:连接OD,如图,根据切线的性质得OD⊥DE,而DE⊥AC,则可判断OD∥AC,根据平行线的性质得到∠BOD=∠C,再由等腰三角形的性质得∠B=∠C,则∠B=∠BOD,易得△ODB为等边三角形,得到∠B=60°,然后根据等边三角形的判定即可得到△ABC为等边三角形.
解答: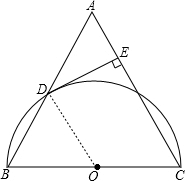 证明:连接OD,如图,
证明:连接OD,如图,
∵DE与半⊙O相切于点D,
∴OD⊥DE,
∵DE⊥AC,
∴OD∥AC,
∴∠BOD=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠BOD,
∴DB=DO,
∵OD=OB,
∴OB=OD=BD,
∴△ODB为等边三角形,
∴∠B=60°,
而△ABC为等腰三角形,
∴△ABC为等边三角形.
 证明:连接OD,如图,
证明:连接OD,如图,∵DE与半⊙O相切于点D,
∴OD⊥DE,
∵DE⊥AC,
∴OD∥AC,
∴∠BOD=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠BOD,
∴DB=DO,
∵OD=OB,
∴OB=OD=BD,
∴△ODB为等边三角形,
∴∠B=60°,
而△ABC为等腰三角形,
∴△ABC为等边三角形.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
 如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )
如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )| A、60° | B、70° |
| C、80° | D、140° |
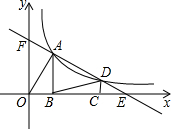 如图,点A,D是函数y=
如图,点A,D是函数y= 如图,在平面直角坐标系中,点O是坐标原点,四边形ABCD是菱形,点B、点C在x轴上,点A在y轴上,BD交y轴于点M,点A的坐标为(0,4),点B的坐标为(-3,0).
如图,在平面直角坐标系中,点O是坐标原点,四边形ABCD是菱形,点B、点C在x轴上,点A在y轴上,BD交y轴于点M,点A的坐标为(0,4),点B的坐标为(-3,0).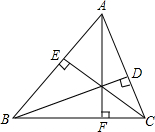 如图,已知AF、BD、CE为△ABC的高.求证:BC2=BE•AB+CD•AC.
如图,已知AF、BD、CE为△ABC的高.求证:BC2=BE•AB+CD•AC. 已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.
已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.