题目内容
已知|m|=3,n=2,且|m-n|=n-m,则n-m= .
考点:绝对值
专题:
分析:根据已知条件确定m的值,然后即可确定两个未知数的差.
解答:解:∵|m|=3,
∴m=±3,
∵|m-n|=n-m,
∴m-n<0,
∵n=2,
∴m=-3,
∴n-m=2-(-3)=2+3=5.
故答案为:5.
∴m=±3,
∵|m-n|=n-m,
∴m-n<0,
∵n=2,
∴m=-3,
∴n-m=2-(-3)=2+3=5.
故答案为:5.
点评:本题考查了绝对值的知识,解题的关键是根据题意确定未知数m的值,比较简单.

练习册系列答案
相关题目
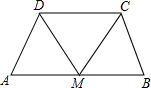 如图,点M是等腰梯形ABCD底边AB的中点,下列说法正确的是( )
如图,点M是等腰梯形ABCD底边AB的中点,下列说法正确的是( )| A、∠DAM=∠DCM |
| B、DM∥BC |
| C、△AMD≌△BMC |
| D、△AMD≌△DMC |
若y=mx2+nx-p(其中m,n,p是常数)为二次函数,则( )
| A、m,n,p均不为0 |
| B、m≠0,且n≠0 |
| C、m≠0 |
| D、m≠0,或p≠0 |
 已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.
已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.
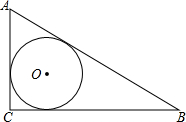 如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为c,a,b.求△ABC的内切圆半径r.
如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为c,a,b.求△ABC的内切圆半径r. 已知,如图,A,B分别为数轴上的两点,A点对应的数是-35,B点对应的数是85.
已知,如图,A,B分别为数轴上的两点,A点对应的数是-35,B点对应的数是85.