题目内容
17. 已知:在锐角三角形ABC中,O是外心,H是垂心,O′,O″是O关于AB,AC的对称点,求证:四边形AO′HO″是菱形.
已知:在锐角三角形ABC中,O是外心,H是垂心,O′,O″是O关于AB,AC的对称点,求证:四边形AO′HO″是菱形.
分析 作OM⊥BC交BC于点M,连接OO′,OO″分别交AB,AC于点DN,连接BO,DN,O′O″,AH,其中O′O″与AH交于点E,根据O′,O″是O关于AB,AC的对称点得到AO′=AO,AO″=AO,从而得到AO′=AO″,然后分别证得△AO′E∽△OBM,△AO′E≌△OBM,从而得到AO′=AO″=O′H=O″H,证得四边形AO′HO″是菱形.
解答  证明:如图,作OM⊥BC交BC于点M,连接OO′,OO″分别交AB,AC于点DN,连接BO,DN,O′O″,AH,其中O′O″与AH交于点E,
证明:如图,作OM⊥BC交BC于点M,连接OO′,OO″分别交AB,AC于点DN,连接BO,DN,O′O″,AH,其中O′O″与AH交于点E,
∵O′,O″是O关于AB,AC的对称点,
∴AO′=AO,AO″=AO,
∴AO′=AO″,
∵H是垂心,
∴AH⊥BC,
∴AH∥OM,
∵DN是△ABC和△OO′O″的中位线,
∴BC∥O′O″,
∴AH⊥BC,
∵BC∥O′O″,AH∥OM,
∴△AO′E∽△OBM,
∵O′是O关于AB的对称点,
∴AO′=OB,
∴△AO′E≌△OBM,
∴AH=OM,
∵AH=2OM(三角形一个顶点到垂心的距离等于外心到对边距离的2倍),
∴O′O″是AH的垂直平分线,
∴AO′=O′H,AO″=O″H,
∴AO′=AO″=O′H=O″H,
∴四边形AO′HO″是菱形.
点评 本题考查了三角形的五心,能够了解三角形的垂心及外心的性质是解答本题的关键,难点是正确的构造辅助线,难度不大.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
8.对于△ABC,下列叙述错误的是( )
| A. | 如果∠A=∠B=∠C,那么△ABC一定是锐角三角形 | |
| B. | 如果∠A=∠B+∠C,那么△ABC一定是直角三角形 | |
| C. | 如果∠A:∠B:∠C=1:3:5,那么△ABC是钝角三角形 | |
| D. | 如果∠A=40°,∠B=3∠C,那么△ABC是锐角三角形 |
12.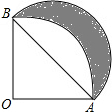 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$π | C. | $\frac{1}{8}$π | D. | π |
6.代数式2x+7与-4x+2互为相反数,则x值为( )
| A. | 9 | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
7.暑假快到了,父母找算带兄妹俩去某个景点旅游一次,长长见识,可哥哥坚持去黄山,妹妹坚持去泰山,争执不下,父母为了公平起见,决定设计一款游戏,若哥哥赢了就去黄山,妹妹赢了就去泰山.下列游戏中,不能选用的是( )
| A. | 掷一枚硬币,正面向上哥哥赢,反面向上妹妹赢 | |
| B. | 同时掷两枚硬币,两枚都正面向上,哥哥赢,一正一反向上妹妹赢 | |
| C. | 掷一枚骰子,向上的一面是奇数则哥哥赢,反之妹妹赢 | |
| D. | 在不透明的袋子中装有两黑两红四个球,除颜色外,其余均相同,随机摸出一个是黑球则哥哥赢,是红球则妹妹赢 |
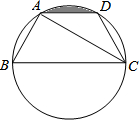 如图所示,已知点A、B、C、D都在同一个圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为20.
如图所示,已知点A、B、C、D都在同一个圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为20.