题目内容
9.观察下列各式21-20=20 22-21=21 23-22=22 24-23=23….
①探索式子的规律,试写出第n个等式2n-2n-1=2n-1;
②计算2m-2m-1,并运用该结果,计算22000-21999-21998-…-2;
③计算:20+21+22+23+24+…+22015.
分析 ①根据式子的规律,可得2n-2n-1=2n-1;
②利用①的结论递推得出答案即可;
③把式子乘(2-1)递推得出答案即可.
解答 解:①∵21-20=20,②22-21=21,③23-22=22…
∴第n(n为正整数)个等式可表示为:2n-2n-1=2n-1(n为正整数).
②22000-21999-21998-…-2
=21999-21998-…-2
=21998-…-2
=2.
③20+21+22+23+24+…+22015
=(2-1)(20+21+22+23+24+…+22015)
=21+22+23+24+…+22016-(20+21+22+23+24+…+22015)
=22016-1.
点评 此题主要考查了数字变化规律,根据已知得出数字次数的变化规律是解题关键.

练习册系列答案
相关题目
18.关于多项式-2x2y+3xy-1,下列说法正确的是( )
| A. | 次数是3 | B. | 常数项是1 | C. | 次数是5 | D. | 三次项是2x2y |
19.已知抛一枚均匀硬币正面朝上的概率为$\frac{1}{2}$,下列说法错误的是( )
| A. | 大量反复抛一均匀硬币,平均100次出现正面朝上50次 | |
| B. | 连续抛一均匀硬币10次都可能正面朝上 | |
| C. | 连续抛一均匀硬币2次必有1次正面朝上 | |
| D. | 通过抛一均匀硬币确定谁先发球的比赛规则是公平的 |
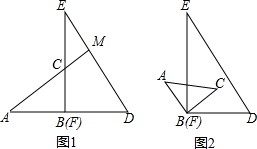
 已知:在锐角三角形ABC中,O是外心,H是垂心,O′,O″是O关于AB,AC的对称点,求证:四边形AO′HO″是菱形.
已知:在锐角三角形ABC中,O是外心,H是垂心,O′,O″是O关于AB,AC的对称点,求证:四边形AO′HO″是菱形. 如图,△ABC中,D、E、F为BC、AD、BE的中点,若△CEF的面积是3,则△ABC的面积是12.
如图,△ABC中,D、E、F为BC、AD、BE的中点,若△CEF的面积是3,则△ABC的面积是12.