题目内容
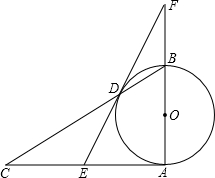 如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.∠F=30°,BF=1,求△ABC外接圆的半径.
如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.∠F=30°,BF=1,求△ABC外接圆的半径.考点:三角形的外接圆与外心
专题:
分析:首先求出△AED是等边三角形,进而得出∠DBG=60°,∠DBG=60°,再利用锐角三角函数关系求出DG以及AD的长,进而得出AB的长.
解答: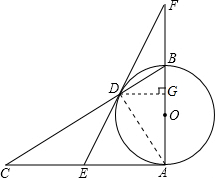 解:连接AD,过点D作DG⊥BA于点G,
解:连接AD,过点D作DG⊥BA于点G,
∵AB是⊙O的直径,
∴∠ADB=90°,则∠CDA=90°,
∵E为AC的中点,
∴DE=AE=EC,
∵∠CAB=90°,∠F=30°,
∴∠AEF=60°,AE=
EF,
∴△AED是等边三角形,
∴AD=DE,DE=DF,
∴DF=AD,
则∠DAF=30°,∠DBG=60°,∠DBG=60°,
故设DG=x,则DF=2x,FG=
x,
有BG=
x-1,
则tan60°=
=
=
,
解得:x=
,
则AD=
,故cos30°=
,
解得:AB=2.
故△ABC外接圆的半径为:1.
 解:连接AD,过点D作DG⊥BA于点G,
解:连接AD,过点D作DG⊥BA于点G,∵AB是⊙O的直径,
∴∠ADB=90°,则∠CDA=90°,
∵E为AC的中点,
∴DE=AE=EC,
∵∠CAB=90°,∠F=30°,
∴∠AEF=60°,AE=
| 1 |
| 2 |
∴△AED是等边三角形,
∴AD=DE,DE=DF,
∴DF=AD,
则∠DAF=30°,∠DBG=60°,∠DBG=60°,
故设DG=x,则DF=2x,FG=
| 3 |
有BG=
| 3 |
则tan60°=
| DG |
| BG |
| x | ||
|
| 3 |
解得:x=
| ||
| 2 |
则AD=
| 3 |
| ||
| AB |
解得:AB=2.
故△ABC外接圆的半径为:1.
点评:此题主要考查了三角形外接圆的性质以及直角三角形的性质和锐角三角函数关系等知识,得出△AED是等边三角形是解题关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
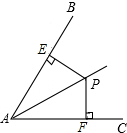 如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PF,则下列哪一个能作为△PEA≌△PFA的理由( )
如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PF,则下列哪一个能作为△PEA≌△PFA的理由( )| A、HL | B、AAS |
| C、SSS | D、ASA |
 如图所示,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于点D,此△ABC叫做“黄金三角形”,求证:BC2=CD•CA.
如图所示,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于点D,此△ABC叫做“黄金三角形”,求证:BC2=CD•CA.