题目内容
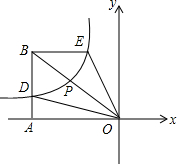
已知点A、B在直线y=-x的图象上,且点A、B是关于原点的对称点,P的坐标为(-2,-1),若△ABP的面积为3,求点A的坐标.
考点:一次函数图象上点的坐标特征
专题:
分析:根据点A、B在直线y=-x的图象上,且点A、B是关于原点的对称点,可知OP把三角形APB分成相等的两个三角形,设出A(x,-x),然后根据S△AOP=S梯形ADEP-S△AOD-S△POE即可求得.
解答: 解:∵点A、B在直线y=-x的图象上,且点A、B是关于原点的对称点,
解:∵点A、B在直线y=-x的图象上,且点A、B是关于原点的对称点,
∴A点在第二象限或第四象限,
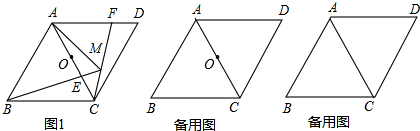
当在二象限时,如图所示,
连接OP,作AD⊥y轴于D,PE⊥y轴于E,设A(x,-x),
∵△ABP的面积为3,
∴△AOP的面积为
,
∵S梯形ADEP=
×(-x+2)(-x+1),S△AOD=
x2,S△POE=
×2×1=1,
∴S△AOP=S梯形ADEP-S△AOD-S△POE=
×(-x+2)(-x+1)-
x2-1=
,
解得,x=-1,
∴A(-1,1),
当在第四象限时,A(1,-1),
∴点A的坐标为(-1,1)或(1,-1).
 解:∵点A、B在直线y=-x的图象上,且点A、B是关于原点的对称点,
解:∵点A、B在直线y=-x的图象上,且点A、B是关于原点的对称点,∴A点在第二象限或第四象限,
当在二象限时,如图所示,
连接OP,作AD⊥y轴于D,PE⊥y轴于E,设A(x,-x),
∵△ABP的面积为3,
∴△AOP的面积为
| 3 |
| 2 |
∵S梯形ADEP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOP=S梯形ADEP-S△AOD-S△POE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解得,x=-1,
∴A(-1,1),
当在第四象限时,A(1,-1),
∴点A的坐标为(-1,1)或(1,-1).
点评:本题考查了坐标与图形性质,三角形的面积,根据△ABP被OP分成的两个三角形的面积相等的三角形求解简便.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 如图,⊙O的半径为5,弦AB=8,则圆上到弦AB所在的直线距离为2的点有( )个.
如图,⊙O的半径为5,弦AB=8,则圆上到弦AB所在的直线距离为2的点有( )个.| A、1 | B、2 | C、3 | D、0 |
 如图,双曲线y=
如图,双曲线y= 如图,AB=DE=GH=MN=2,其余各短边长为1,且图中的角都是直角,请建立适当的直角坐标系,并写出各个顶点的坐标.
如图,AB=DE=GH=MN=2,其余各短边长为1,且图中的角都是直角,请建立适当的直角坐标系,并写出各个顶点的坐标. 在如图所示的平面直角坐标系中描出下列各点:
在如图所示的平面直角坐标系中描出下列各点: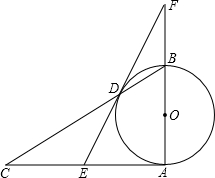 如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.∠F=30°,BF=1,求△ABC外接圆的半径.
如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.∠F=30°,BF=1,求△ABC外接圆的半径.