题目内容
 如图所示,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于点D,此△ABC叫做“黄金三角形”,求证:BC2=CD•CA.
如图所示,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于点D,此△ABC叫做“黄金三角形”,求证:BC2=CD•CA.考点:黄金分割
专题:证明题
分析:根据等腰三角形的性质和三角形内角和定理可计算出图中所有角的度数,则得到△DAB和△BDC勾是等腰三角形,再证明△ABC∽△BCD,然后利用相似比易得到结论.
解答:证明:∵AB=AC,
∴∠ABC=∠C,
而∠BAC=36°,
∴∠ABC=∠C=
(180°-36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∴DA=DB,
∵∠BDC=2∠A=72°,
∴BD=BC,
∵∠A=∠CBD,∠C为公共角,
∴△ABC∽△BCD,
∴BC:CD=AC:BC,
∴BC2=CD•CA.
∴∠ABC=∠C,
而∠BAC=36°,
∴∠ABC=∠C=
| 1 |
| 2 |
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∴DA=DB,
∵∠BDC=2∠A=72°,
∴BD=BC,
∵∠A=∠CBD,∠C为公共角,
∴△ABC∽△BCD,
∴BC:CD=AC:BC,
∴BC2=CD•CA.
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点;其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
如果a2-a+1=2,则2a-2a2+1的值为( )
| A、-1 | B、0 | C、1 | D、-2 |
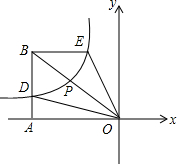 如图,双曲线y=
如图,双曲线y= 在如图所示的平面直角坐标系中描出下列各点:
在如图所示的平面直角坐标系中描出下列各点: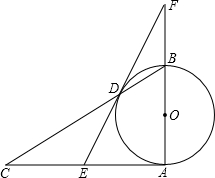 如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.∠F=30°,BF=1,求△ABC外接圆的半径.
如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.∠F=30°,BF=1,求△ABC外接圆的半径.