题目内容
在△ABC中,AB=AC,∠A=90°.
(1)如果S△ABC=1,求AC的长;
(2)如果S△ABC=3,求AC的长.
(1)如果S△ABC=1,求AC的长;
(2)如果S△ABC=3,求AC的长.
考点:等腰直角三角形
专题:
分析:由S△ABC=
AC•AB=
AC2,代入计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:因为S△ABC=
AC•AB=
AC2,
所以(1)当S△ABC=1时,AC2=1,所以AC=1;
(2)当S△ABC=3时,AC2=3,所以AC=
.
| 1 |
| 2 |
| 1 |
| 2 |
所以(1)当S△ABC=1时,AC2=1,所以AC=1;
(2)当S△ABC=3时,AC2=3,所以AC=
| 3 |
点评:本题主要考查等腰直角三角形的性质,正确表示出三角形的面积是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
如果a2-a+1=2,则2a-2a2+1的值为( )
| A、-1 | B、0 | C、1 | D、-2 |
 如图,⊙O的半径为5,弦AB=8,则圆上到弦AB所在的直线距离为2的点有( )个.
如图,⊙O的半径为5,弦AB=8,则圆上到弦AB所在的直线距离为2的点有( )个.| A、1 | B、2 | C、3 | D、0 |
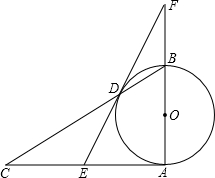 如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.∠F=30°,BF=1,求△ABC外接圆的半径.
如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.∠F=30°,BF=1,求△ABC外接圆的半径.